Hai cầu thủ sút phạt đền. Mỗi người đá 1 lần với xác suất ghi bàn tương ứng là 0,8 và 0,7 . Tính xác suất để có ít nhất 1 cầu thủ ghi bàn.
Hai cầu thủ sút phạt đền. Mỗi người đá 1 lần với xác suất ghi bàn tương ứng là 0,8 và 0,7 . Tính xác suất để có ít nhất 1 cầu thủ ghi bàn.
A. \(P(X) = 0,42\).
B. \(P(X) = 0,94\).
C. \(P(X) = 0,234\).
D. \(P(X) = 0,9\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \(A\) là biến cố "Cầu thủ thứ nhất ghi bàn"; \(B\) là biến cố "Cầu thủ thứ hai ghi bàn"; \(X\) là biến cố "Ít nhất một trong hai cầu thủ ghi bàn".
- Cầu thủ thứ nhất ghi bàn và cầu thủ hai không ghi bàn là \(A\bar B\), ta có:
\(P(A\bar B) = P(A) \cdot P(\bar B) = 0,8 \cdot 0,3 = 0,24.{\rm{ }}\)
- Cầu thủ thứ nhất không ghi bàn và cầu thủ hai ghi bàn là \(\bar AB\), ta có:
\(P(\bar AB) = P(\bar A) \cdot P(B) = 0,2 \cdot 0,7 = 0,14.{\rm{ }}\)
- Cả hai cầu thủ ghi bàn là \(AB\), ta có: \(P(AB) = P(A) \cdot P(B) = 0,8 \cdot 0,7 = 0,56\).
Biến cố để có ít nhất một cầu thủ ghi bàn là \(X = A\bar B \cup \bar AB \cup AB\).
Xác suất để có ít nhất một cầu thủ ghi bàn là:
\(P(X) = P(A\bar B) + P(\bar AB) + P(AB) = 0,24 + 0,14 + 0,56 = 0,94.\)
Chọn B.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: \((SC,(SAB)) \approx {12,1^0}\)
Lời giải
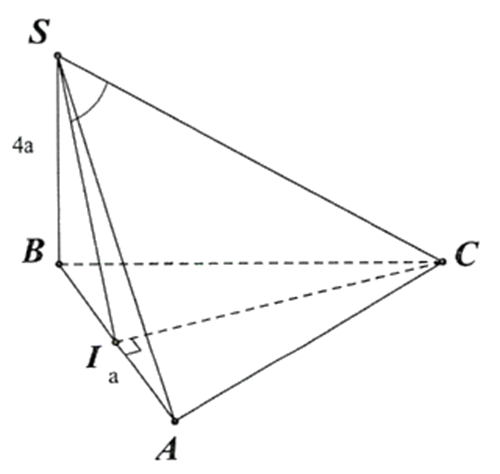
Kẻ \(CI \bot AB \Rightarrow I\) là trung điểm \(AB\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{CI \bot AB}\\{CI \bot SB}\end{array} \Rightarrow CI \bot (SAB)} \right.\) tại \(I\) và \(SC\) cắt mp\((SAB)\) tại \(S\)
\( \Rightarrow SI\) là hình chiếu của \(SC\) trên mp \((SAB)\)
\( \Rightarrow (SC,(SAB)) = (SC,SI) = \widehat {CSI}\)
Ta có: \(IC = \frac{{a\sqrt 3 }}{2}\)
Ta có: \(SC = \sqrt {S{B^2} + B{C^2}} = \sqrt {{{(4a)}^2} + {a^2}} = \sqrt {17} a\)
Xét \(\Delta SCI\) vuông tại \(I\) : \(\sin \widehat {CSI} = \frac{{CI}}{{SC}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\sqrt {17} a}} = \frac{{\sqrt {51} }}{{34}} \Rightarrow \widehat {CSI} \approx {12,1^0}\)
Vậy \((SC,(SAB)) \approx {12,1^0}\).
Lời giải
Trả lời: \(\frac{{36}}{{121}}\)
Ta có sơ đồ cây như sau:
Trong đó: Đ là biến cố "Lấy được quả bóng màu đỏ”, X là biến cố "Lấy được quả bóng màu xanh".
Dựa vào sơ đồ cây, xác suất lấy 2 bóng xanh sau 2 lượt là \({\left( {\frac{6}{{11}}} \right)^2} = \frac{{36}}{{121}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SAB} \right)\) là đoạn \(BC\).
Đúng
Sai
b) \[BC \bot \left( {SAB} \right)\].
Đúng
Sai
c) Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\) là đoạn \(AB\).
Đúng
Sai
d) \[SB \bot BC\].
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập