Bộ 10 đề thi cuối kì 2 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 02
4.6 0 lượt thi 16 câu hỏi 45 phút
🔥 Đề thi HOT:
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
49.5 K lượt thi
30 câu hỏi
Bài tập Giới hạn cơ bản, nâng cao có lời giải (P1)
15.2 K lượt thi
25 câu hỏi
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
19.9 K lượt thi
30 câu hỏi
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
7.9 K lượt thi
12 câu hỏi
Bộ 19 đề thi Giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 1
2.1 K lượt thi
19 câu hỏi
20 câu trắc nghiệm Toán 11 Kết nối tri thức Mẫu số liệu ghép nhóm có đáp án
2.6 K lượt thi
20 câu hỏi
160 Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P4)
10.7 K lượt thi
30 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A.\({a^{\frac{5}{6}}}\).
B.\({a^{\frac{7}{6}}}\).
C.\({a^{\frac{4}{3}}}\).
D.\({a^{\frac{6}{7}}}\).
Lời giải
Với \[a > 0\], ta có \[{a^{\frac{2}{3}}}\sqrt a = {a^{\frac{2}{3}}}.{a^{\frac{1}{2}}} = {a^{\frac{2}{3} + \frac{1}{2}}} = {a^{\frac{7}{6}}}\].
Câu 2
A. \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^2}\).
B. \(y = {\left( {\sqrt 2 } \right)^x}\).
C. \(y = {\left( {\frac{1}{3}} \right)^x}\).
D. \(y = {3^x}\).
Lời giải
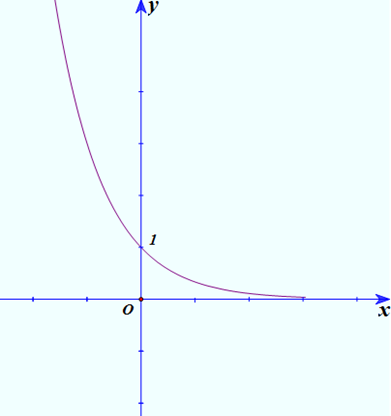
Đồ thị hàm số ở hình vẽ là đồ thị của hàm số mũ có dạng \(y = {a^x}\). Loại đáp án A
Dựa vào đồ thị ta thấy hàm số nghịch biến trên \(\mathbb{R}\) nên \(0 < a < 1\). Loại đáp án B, D
Vậy đồ thị trong hình vẽ là đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\).
Câu 3
A. \(CD \bot AB\).
B. \(AC \bot BD\).
C. \(BC \bot AD\).
D. \(BC \bot CD\).
Lời giải
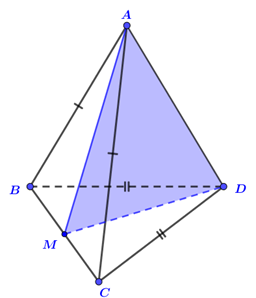
Gọi \(M\) là trung điểm \(BC\). Do tam giác \(1\) cân tại \(A\) và tam giác \(DBC\) cân tại \(D\) nên, có: \(\left\{ \begin{array}{l}BC \bot DM\\BC \bot AM\end{array} \right. \Rightarrow BC \bot AD\).
Câu 4
A. \[2\].
B. \[\sqrt 3 \].
C. \[1\].
D. \[\sqrt 2 \].
Lời giải
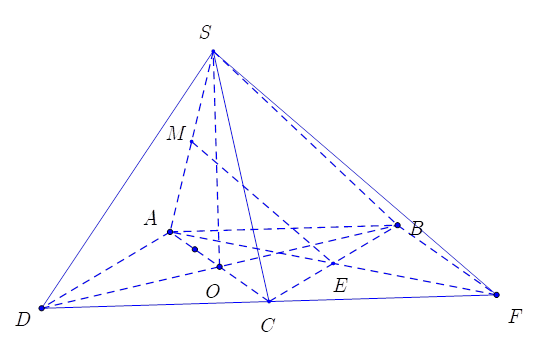
Dựng hình bình hành \(ABFC\).
Ta có \(EM\;{\rm{//}}\;SF\)nên góc giữa \(EM\) và \(\left( {SBD} \right)\) bằng góc giữa \(SF\) và \(\left( {SBD} \right)\).
\(FB\;{\rm{//}}\;AC\)\( \Rightarrow FB \bot \left( {SBD} \right)\) do đó góc giữa \(SF\) và \(\left( {SBD} \right)\) bằng góc \(\widehat {FSB}\).
Ta có \(\tan \widehat {FSB} = \frac{{BF}}{{SB}} = \frac{{AC}}{{SB}} = \sqrt 2 \). Vậy chọn D.
Câu 5
A. \(BC \bot AH\).
B. \(SA \bot AC\).
C. \(HK \bot SC\).
D. \(AK \bot BD\).
Lời giải
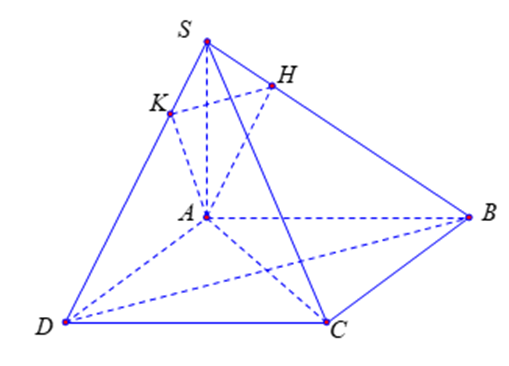
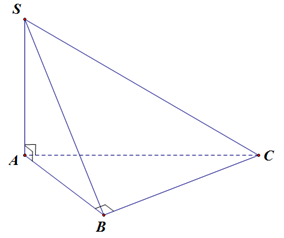
Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\end{array} \right.\) nên \[SA \bot \left( {ABCD} \right)\]
Suy ra \[SA \bot AC\] (B đúng); \(SA \bot BC\); \(SA \bot BD\).
Mặt khác \(BC \bot AB\) nên \(BC \bot \left( {SAB} \right)\) suy ra \[BC \bot AH\] (A đúng).
và \(BD \bot AC\) nên \(BD \bot \left( {SAC} \right)\) suy ra \[BD \bot SC\];
Đồng thời \(HK\;{\rm{//}}\;BD\) nên \(HK \bot SC\) (C đúng).
Vậy mệnh đề sai là \(AK \bot BD\) (vì không đủ điều kiện chứng minh).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{{{a^3}}}{2}\).
B. \(\frac{{{a^3}}}{3}\).
C. \(\frac{{{a^3}}}{4}\).
D. \(\frac{{2{a^3}}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \(P(X) = 0,42\).
B. \(P(X) = 0,94\).
C. \(P(X) = 0,234\).
D. \(P(X) = 0,9\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(\frac{2}{3}\).
B. \(\frac{1}{6}\).
C. \(\frac{1}{3}\).
D. \(\frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \(y' = {17^{ - x}}\ln 17\).
B. \(y' = - x{.17^{ - x - 1}}\).
C. \(y' = - {17^{ - x}}\).
D. \(y' = - {17^{ - x}}\ln 17\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \[12{\rm{m/}}{{\rm{s}}^2}\].
B. \[ - 6{\rm{m/}}{{\rm{s}}^2}\].
C. \[ - 12{\rm{m/}}{{\rm{s}}^2}\].
D. \[6{\rm{m/}}{{\rm{s}}^2}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Theo kết quả khảo sát ở một trường học về số học sinh yêu thích một loại nước giải khát \(A\) được cho bởi bảng sau:
Lớp
Thích
Không thích
Số học sinh nam
Số học sinh nữ
Số học sinh nam
Số học sinh nữ
11A
23
12
5
10
11B
25
15
6
12
11C
20
15
8
15
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Theo kết quả khảo sát ở một trường học về số học sinh yêu thích một loại nước giải khát \(A\) được cho bởi bảng sau:
|
Lớp |
Thích |
Không thích |
||
|
Số học sinh nam |
Số học sinh nữ |
Số học sinh nam |
Số học sinh nữ |
|
|
11A |
23 |
12 |
5 |
10 |
|
11B |
25 |
15 |
6 |
12 |
|
11C |
20 |
15 |
8 |
15 |
a) Xác suất để chọn được một học sinh nam và một học sinh nữ ở khối lớp 11 mà thích uống nước giải khát \(A\) là \(\frac{{952}}{{4565}}\).
Đúng
Sai
b) Xác suất để chọn được một học sinh nam ở lớp \(11\;A\) và một học sinh nam ở lớp \(11\;B\) không thích nước giải khát \(A\) là \(\frac{1}{{2739}}\).
Đúng
Sai
c) Gọi \(A\) là biến cố: "Học sinh nam thích nước giải khát \(A\) ". Tính được \(P(A) = \frac{{42}}{{79}}\).
Đúng
Sai
d) Việc thích uống nước giải khát \(A\) có phụ thuộc vào giới tính.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
a) Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SAB} \right)\) là đoạn \(BC\).
Đúng
Sai
b) \[BC \bot \left( {SAB} \right)\].
Đúng
Sai
c) Khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\) là đoạn \(AB\).
Đúng
Sai
d) \[SB \bot BC\].
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
a) Đồ thị hai hàm số đối xứng nhau qua đường thẳng \(y = - x\).
Đúng
Sai
b) Tập xác định của hai hàm số trên là \(\mathbb{R}\).
Đúng
Sai
c) Đồ thị của hai hàm số cắt nhau tại đúng một điểm.
Đúng
Sai
d) Hai hàm số trên đều nghịch biến trên tập xác định của nó.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) \(f\left( x \right)\)liên tục tại \(x = - 1.\)
Đúng
Sai
b) \(f\left( x \right)\)có đạo hàm tại \(x = - 1.\)
Đúng
Sai
c) \(f\left( { - 1} \right) = 0.\)
Đúng
Sai
d) \(f\left( x \right)\)đạt giá trị nhỏ nhất tại \(x = - 1.\)
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập