Bộ 10 đề thi cuối kì 2 Toán 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 07
28 người thi tuần này 4.6 573 lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
A. \({\log _9}1125 = 1 + \frac{3}{{2a}}\).
Lời giải
Ta có: \({\log _9}1125 = {\log _{{3^2}}}\left( {{5^3}{{.3}^2}} \right) = {\log _{{3^2}}}{5^3} + {\log _{{3^2}}}{3^2} = \frac{3}{2}{\log _3}5 + 1 = \frac{3}{2}.\frac{1}{{{{\log }_5}3}} + 1 = 1 + \frac{3}{{2a}}\).
Câu 2
A. \(x = 4\).
Lời giải
Ta có \({2^{x - 1}} = 8 \Leftrightarrow x - 1 = 3 \Leftrightarrow x = 4\).
Câu 3
A. \[{75^0}\].
Lời giải
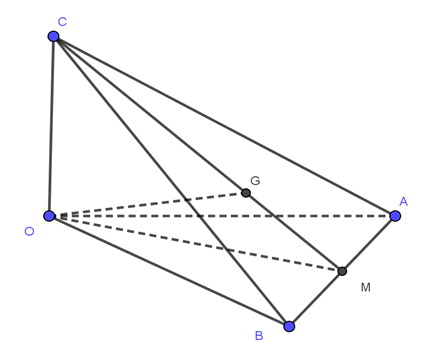
Gọi M là trung điểm \(AB\), ta có \(OM \bot AB\). Mặt khác dễ thấy \(OC \bot \left( {OAB} \right) \Rightarrow OC \bot AB\)
\( \Rightarrow AB \bot \left( {OCM} \right) \Rightarrow AB \bot OG \Rightarrow \left( {\widehat {OG,AB}} \right) = {90^0}\)
Câu 4
Lời giải
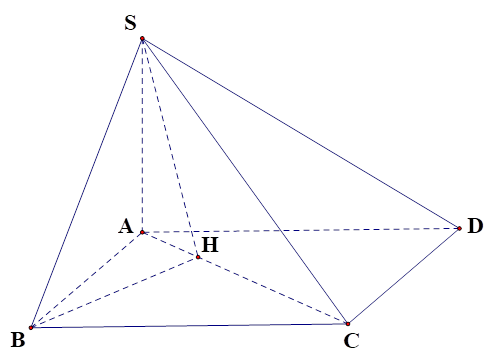
Kẻ \[BH \bot AC\] và \[H \in AC\]\[ \Rightarrow \]\[BH \bot \left( {SAC} \right)\].
\[SH\] là hình chiếu của \[BH\] trên mặt phẳng \[\left( {SAC} \right)\].
Góc giữa \[SB\] và mặt phẳng \[\left( {SAC} \right)\] là \[\widehat {BSH}\].
Ta có \[BH = \frac{{AB.BC}}{{\sqrt {A{B^2} + B{C^2}} }} = \frac{{a\sqrt 3 }}{2}\], \[SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 3 \].
Trong tam giác vuông \[SBH\] ta có \[\sin \widehat {BSH} = \frac{{BH}}{{SB}} = \frac{1}{2}\]\[ \Rightarrow \widehat {BSH} = 30^\circ \].
Câu 5
A. \[\left( {SCD} \right) \bot \left( {SAD} \right) \cdot \]
B. \[\left( {SBC} \right) \bot \left( {SIA} \right) \cdot \]
Lời giải
Chọn A
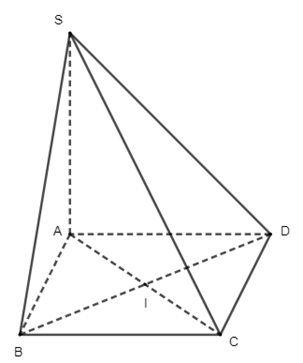
Ta có:
\[CD \bot AD\](vì \(ABCD\) là hình chữ nhật)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot CD\)
\(SA \cap AD = A\)
\(SA,AD \subset \left( {SAD} \right)\)
\( \Rightarrow CD \bot \left( {SAD} \right)\)
Mà \[CD \subset \left( {SCD} \right)\] nên \[\left( {SCD} \right) \bot \left( {SAD} \right)\].
Câu 6
A. \(2\sqrt 5 a\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(V = \frac{{2{a^3}}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 0,3 .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(\frac{1}{5}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \[27\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
A. \(y = 9x - 7\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
An và Huy lần lượt lấy ngẫu nhiên các mảnh giấy có kích thước giống nhau được đánh số từ 1 đến 9 trong một hộp kín. Gọi biến cố \(A\): "An lấy được mảnh giấy đánh số chẵn". Biến cố \(B\): "Huy lấy được mảnh giấy đánh số chẵn". Biến cố \(C\): "An lấy được mảnh giấy đánh số 8". Khi đó:
a) \(P(A) = \frac{4}{9}\)
b) \(P(C) = \frac{1}{9}\)
c) \(P(B) = \frac{4}{9}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
a) \[O.ABC\] là hình chóp đều.
b) Tam giác \[ABC\] có diện tích \[S = \frac{{{a^2}\sqrt 3 }}{2}\].
c) Tam giác \[ABC\] có chu vi \[2p = \frac{{3a\sqrt 2 }}{2}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
a) Phương trình có nghiệm dương nếu \[m > 0\].
b) Phương trình luôn có nghiệm với mọi \[m\].
c) Phương trình luôn có nghiệm duy nhất \[x = {\log _3}\left( {m + 1} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) Vận tốc của chuyển động bằng \(0\)khi \(t = 0\,{\rm{s}}\) hoặc \(t = 2\,{\rm{s}}.\)
b) Gia tốc của chuyển động tại thời điểm \(t = 3\,{\rm{s}}\) là \(12\;{\rm{m/}}{{\rm{s}}^2}\).
c) Gia tốc của chuyển động bằng \(0\;{\rm{m/}}{{\rm{s}}^2}\) khi \(t = 0\,{\rm{s}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.