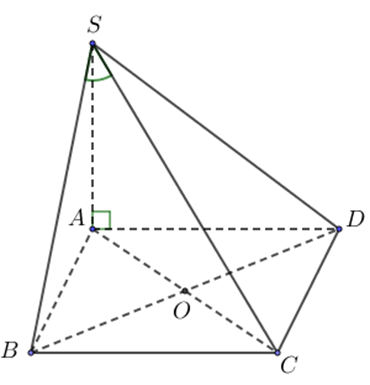
Cho tứ diện \(S.ABC\) trong đó \(SA,SB,SC\) vuông góc với nhau từng đôi một và \(SA = 3a,SB = a,SC = 2a\). Tính khoảng cách từ \(A\) đến đường thẳng \(BC\).
Cho tứ diện \(S.ABC\) trong đó \(SA,SB,SC\) vuông góc với nhau từng đôi một và \(SA = 3a,SB = a,SC = 2a\). Tính khoảng cách từ \(A\) đến đường thẳng \(BC\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: \(d(A,BC) = \frac{{7\sqrt 5 }}{5}a\)
Lời giải
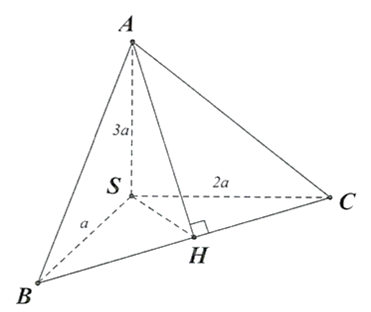
Kẻ \(AH \bot BC\) tại \(H \Rightarrow d(A,BC) = AH\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot SA}\\{BC \bot AH}\end{array} \Rightarrow BC \bot (SAH) \Rightarrow BC \bot SH} \right.\)
Ta có: \(SH = \frac{1}{{\sqrt {\frac{1}{{S{C^2}}} + \frac{1}{{S{B^2}}}} }} = \frac{1}{{\sqrt {\frac{1}{{{{(2a)}^2}}} + \frac{1}{{{a^2}}}} }} = \frac{{2\sqrt 5 }}{5}a\)
Ta có: \(AH = \sqrt {S{A^2} + S{H^2}} = \sqrt {{{(3a)}^2} + {{\left( {\frac{{2\sqrt 5 }}{5}a} \right)}^2}} = \frac{{7\sqrt 5 }}{5}a\)
Vậy \(d(A,BC) = \frac{{7\sqrt 5 }}{5}a\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: \( \approx {62,7^0}\)
Lời giải
Kẻ \(BI \bot AC\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BI \bot AC}\\{BI \bot SA}\end{array} \Rightarrow BI \bot (SAC)} \right.\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{(SAC) \cap (SBC) = SC}\\{{\mathop{\rm Trong}\nolimits} \,(SAC),IH \bot SC \Rightarrow [A,SC,B] = \widehat {IHB}}\\{{\mathop{\rm Trong}\nolimits} \,(SBC),BH \bot SC}\end{array}} \right.\)
Ta có:
Xét \(\Delta BH\) vuông tại \(I:\tan \widehat {BHI} = \frac{{BI}}{{HI}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\frac{{\sqrt 5 }}{5}a}} = \frac{{\sqrt {15} }}{2} \Rightarrow \widehat {BHI} \approx {62,7^0}\)
Câu 2
A. \(90^\circ \).
B. \(60^\circ \).
C. \(30^\circ \).
D. \(45^\circ \).
Lời giải
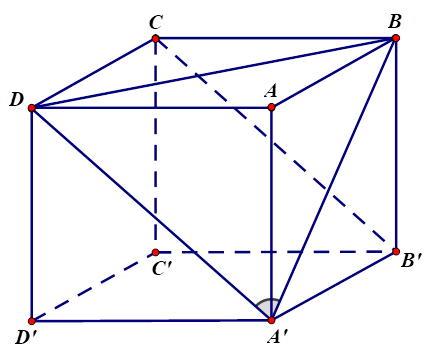
Ta có \(B'C\;{\rm{//}}\;A'D\)\( \Rightarrow \widehat {\left( {A'B;B'C} \right)} = \widehat {\left( {A'B;A'D} \right)}\)\( = \widehat {DA'B}\).
Xét \(\Delta DA'B\) có \(A'D = A'B\)\( = BD\) nên \(\Delta DA'B\) là tam giác đều.
Vậy \(\widehat {DA'B}\)\( = 60^\circ \).
Câu 3
A. \(\left( {SBC} \right) \bot \left( {SAB} \right)\).
B. \(\left( {SAB} \right) \bot \left( {ABCD} \right)\).
C. \(\left( {SAC} \right) \bot \left( {ABCD} \right)\).
D. \(\left( {SAC} \right) \bot \left( {SAD} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) \[{y^2} + {\left( {y'} \right)^2} = 4\].
Đúng
Sai
b) \(4y + y'' = 0\).
Đúng
Sai
c) \[4y - y'' = 0\].
Đúng
Sai
d) \[y = y'\tan 2x\].
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\frac{1}{{\sqrt {14} }}\].
B. \[\frac{{\sqrt 2 }}{2}\].
C. \[\frac{{\sqrt 3 }}{2}\].
D. \[\frac{1}{5}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập