Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(a,\widehat {BAD} = 120,SA \bot (ABCD)\) và \(SA = \sqrt 3 a\). Tính góc giữa đường thẳng \(SC\) và mặt phẳng \((SAD)\)?
Cho hình chóp \(S.ABCD\) có đáy là hình thoi cạnh \(a,\widehat {BAD} = 120,SA \bot (ABCD)\) và \(SA = \sqrt 3 a\). Tính góc giữa đường thẳng \(SC\) và mặt phẳng \((SAD)\)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trả lời: \( \approx {64,3^0}\)
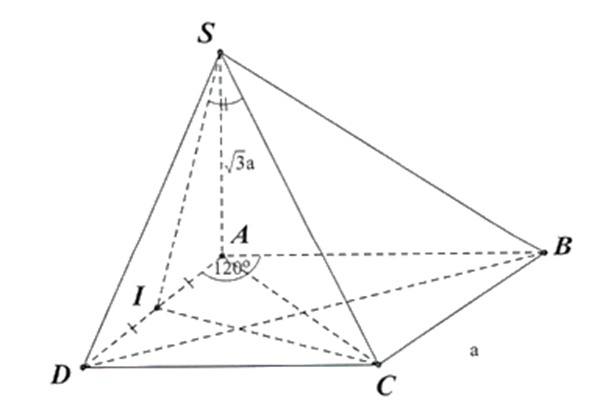
Xét \(\Delta ADC\) cân tại \(D\), có \(\widehat {{\mkern 1mu} D{\mkern 1mu} } = {60^^\circ }\) nên \(\Delta ADC\) đều.
Kẻ \(CI \bot AD\)
Ta có: \(CI \bot SA \Rightarrow CI \bot (SAD)\) tại \(I\) và \(SC\) cắt mp \((SAD)\) tại \(S\) \( \Rightarrow SI\) là hình chiếu của \(SC\) trên mp\((SAD)\)
\( \Rightarrow (SC,(SAD)) = (SC,SI) = \widehat {CSI}\)
Ta có: \(SI = \sqrt {S{A^2} + A{I^2}} = \sqrt {{{(a\sqrt 3 )}^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{\sqrt {13} }}{2}a\)
Xét \(\Delta SCI\) vuông tại \(I:\tan \widehat {CSI} = \frac{{SI}}{{IC}} = \frac{{\frac{{a\sqrt {13} }}{2}}}{{\frac{{\sqrt 3 a}}{2}}} = \frac{{\sqrt {39} }}{3} \Rightarrow \widehat {CSI} \approx {64,3^0}\)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Gieo một con xúc xắc cân đối và đồng chất 2 lần liên tiếp. Gọi biến cố \(A\) là "Số chấm xuất hiện trên xúc xắc là số lẻ" và biến cố \(B\) là "Số chấm xuất hiện trên xúc xắc ở lần thứ hai lớn hơn 3 ".
Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai
Gieo một con xúc xắc cân đối và đồng chất 2 lần liên tiếp. Gọi biến cố \(A\) là "Số chấm xuất hiện trên xúc xắc là số lẻ" và biến cố \(B\) là "Số chấm xuất hiện trên xúc xắc ở lần thứ hai lớn hơn 3 ".
a) Biến cố xung khắc với biến cố \(A\) là biến cố \(\bar A\) được phát biểu như sau: "Số chấm xuất hiện trên xúc xắc ở lần thứ nhất là số chẵn"
Đúng
Sai
b) \(P(\bar A) = \frac{{n(\bar A)}}{{n(\Omega )}} = \frac{1}{2}\)
Đúng
Sai
c) \(P(\bar B) = P\left( {\overline A } \right)\)
Đúng
Sai
d) \(P(\overline {AB} ) = \frac{{n(\overline {AB} )}}{{n(\Omega )}} = \frac{1}{3}\)
Đúng
Sai
Lời giải
|
a) Đúng |
b) Đúng |
c) Đúng |
d) Sai |
a) Biến cố \(\bar A\) là "Số chấm xuất hiện trên xúc xắc ở lần thứ nhất là số chẵn".
Biến cố \(\bar B\) là "Số chấm xuất hiện trên xúc xắc ở lần thứ hai nhỏ hơn hoặc bằng 3 ".
b) \(P(\bar A) = \frac{{n(\bar A)}}{{n(\Omega )}} = \frac{{18}}{{36}} = \frac{1}{2}\).
c) \(P(\bar B) = \frac{{n(\bar B)}}{{n(\Omega )}} = \frac{{18}}{{36}} = \frac{1}{2}.\)
d) \(P(\overline {AB} ) = \frac{{n(\overline {AB} )}}{{n(\Omega )}} = \frac{9}{{36}} = \frac{1}{4}.\)
Lời giải
Chọn C.
Gọi \(n\) (\(n\) là số nguyên dương) là số trận An chơi. Gọi \(A\) là biến cố “An thắng ít nhất 1 trận trong loạt chơi \(n\) trận". Suy ra \(\bar A\) là biến cố: "An thua tất cả \(n\) trận".
Ta có: \(P(A) = 1 - P(\bar A) = 1 - {(0,6)^n}\).
Theo giả thiết:
\(P(A) > 0,95 \Leftrightarrow 1 - {(0,6)^n} > 0,95 \Rightarrow {(0,6)^n} < 0,05 \Rightarrow n > {\log _{0,6}}0,05 \approx 5,86.{\rm{ }}\)
Số nguyên dương \(n\) nhỏ nhất thoả mãn là 6 (An chơi tối thiểu 6 trận).
Câu 3
A. \(\frac{{73}}{{126}}\).
B. \(\frac{{53}}{{126}}\).
C. \(\frac{5}{9}\).
D. \(\frac{{38}}{{63}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[45^\circ \].
B. \[30^\circ \].
C. \[75^\circ \].
D. \[60^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\frac{{a\sqrt 6 }}{3}\).
B. \(\frac{{a\sqrt 3 }}{3}\).
C. \(\frac{{a\sqrt 8 }}{3}\).
D. \(\frac{{a\sqrt 2 }}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập