Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a\),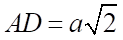 ,
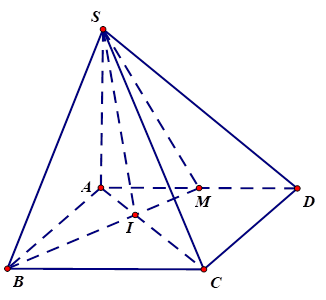
, 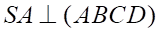 . Gọi \(M\) là trung điểm của \[AD\], \(I\) là giao điểm của \(AC\) và \(BM\). Khẳng định nào sau đây đúng?
. Gọi \(M\) là trung điểm của \[AD\], \(I\) là giao điểm của \(AC\) và \(BM\). Khẳng định nào sau đây đúng?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a\),![]() ,
, ![]() . Gọi \(M\) là trung điểm của \[AD\], \(I\) là giao điểm của \(AC\) và \(BM\). Khẳng định nào sau đây đúng?
. Gọi \(M\) là trung điểm của \[AD\], \(I\) là giao điểm của \(AC\) và \(BM\). Khẳng định nào sau đây đúng?
A. \(\left( {SAC} \right) \bot \left( {SMB} \right)\).
Quảng cáo
Trả lời:
Chọn A
+ Ta có:![]()
+ Xét tam giác vuông \(ABM\) có: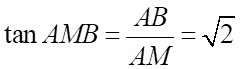 .
.
Xét tam giác vuông \(ACD\) có: 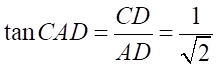 . Ta có:
. Ta có:
\(\cot \widehat {AIM} = \cot \left( {{{180}^0} - \left( {\widehat {AMB} + \widehat {CAD}} \right)} \right) = - \cot \left( {\widehat {AMB} + \widehat {CAD}} \right)\) \[ = - \frac{{1 - \tan \widehat {AMB}.\tan \widehat {CAD}}}{{\tan \widehat {AMB} + \tan \widehat {CAD}}} = 0\]
\( \Rightarrow \widehat {AIM} = {90^0}\) 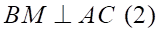
Từ (1) và (2) suy ra:![]() mà
mà ![]() nên
nên ![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: \( \approx {64,3^0}\)
Lời giải
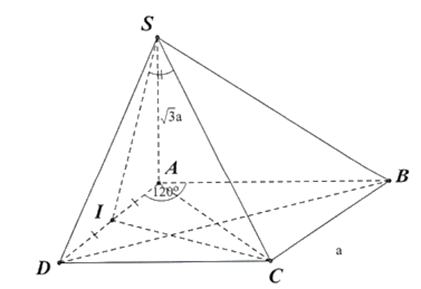
Xét \(\Delta ADC\) cân tại \(D\), có \(\widehat {{\mkern 1mu} D{\mkern 1mu} } = {60^^\circ }\) nên \(\Delta ADC\) đều.
Kẻ \(CI \bot AD\)
Ta có: \(CI \bot SA \Rightarrow CI \bot (SAD)\) tại \(I\) và \(SC\) cắt mp \((SAD)\) tại \(S\) \( \Rightarrow SI\) là hình chiếu của \(SC\) trên mp\((SAD)\)
\( \Rightarrow (SC,(SAD)) = (SC,SI) = \widehat {CSI}\)
Ta có: \(SI = \sqrt {S{A^2} + A{I^2}} = \sqrt {{{(a\sqrt 3 )}^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{\sqrt {13} }}{2}a\)
Xét \(\Delta SCI\) vuông tại \(I:\tan \widehat {CSI} = \frac{{SI}}{{IC}} = \frac{{\frac{{a\sqrt {13} }}{2}}}{{\frac{{\sqrt 3 a}}{2}}} = \frac{{\sqrt {39} }}{3} \Rightarrow \widehat {CSI} \approx {64,3^0}\)
Lời giải
Trả lời: \(\frac{{33}}{{40}}\)
Lời giải
Xác suất để chọn được một học sinh thích môn Ngữ văn hoặc môn Toán: \(\frac{{25 + 20 - 12}}{{40}} = \frac{{33}}{{40}}\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left( { - \infty ;\,2} \right) \cup \left( {3;\, + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Biến cố "Tích hai số ghi trên hai thẻ là một số chẵn" là \(A \cup B\).
b) \(P(A \cup B) = P(A) + P(B)\)
c) \(P(A) < P(B){\rm{ }}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a) \(\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \widehat {SBA}\).
b) \(d\left( {D,\left( {SAC} \right)} \right) = DO\).
c) \[\left( {SC,\left( {SAD} \right)} \right) = \widehat {CSD}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
a) \[f'(2) = 2\]
b) \[f(2) = 2\]
c) \(f\left( 2 \right) + f'\left( 2 \right) = 4\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.