Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt 3 \) Gọi \(\alpha \) là góc tạo bởi giữa đường thẳng \(SB\) và mặt phẳng \(\left( {SAC} \right)\), khi đó \(\alpha \) thỏa mãn hệ thức nào sau đây:
A. \(\cos \alpha = \frac{{\sqrt 2 }}{8}\).
Quảng cáo
Trả lời:
Gọi \(O\) là tâm của đáy \(ABCD\).
Ta có \(BO \bot AC\) và \(BO \bot SA\) nên \(SO\) là hình chiếu của \(SB\) trên \(\left( {SAC} \right)\).
Suy ra \(\alpha = \widehat {BSO}\).
Lại có \(BO = \frac{{a\sqrt 2 }}{2}\), \(SB = \sqrt {S{A^2} + A{B^2}} = 2a\). Suy ra \(\sin \alpha = \frac{{BO}}{{SB}} = \frac{{\sqrt 2 }}{4}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\left( { - \infty ;\,2} \right) \cup \left( {3;\, + \infty } \right)\).
Lời giải
\({\log _{\frac{1}{2}}}\left( {{x^2} - x + 7} \right) > 0\)\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 5x + 7 > 0\\{x^2} - 5x + 7 < 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{\left( {x - \frac{5}{2}} \right)^2} + \frac{3}{4} > 0,\,\forall x \in \mathbb{R}\\{x^2} - 5x + 6 < 0\end{array} \right.\)\( \Rightarrow x \in \left( {2;\,3} \right)\).
Lời giải
Trả lời: \({69,3^^\circ }\)
Lời giải
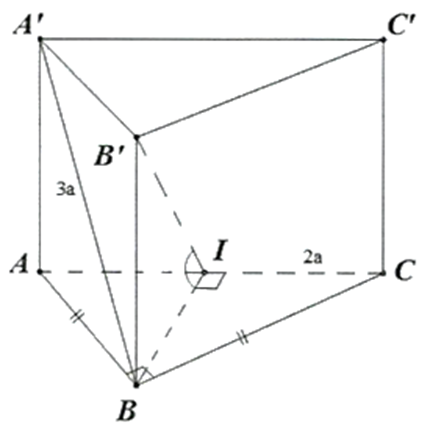
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {{B^\prime }AC} \right) \cap (ABC) = AC}\\{{\mathop{\rm Trong}\nolimits} (ABC),BI \bot AC \Rightarrow [A,SC,B] = \widehat {{B^\prime }IB}}\\{{\mathop{\rm Trong}\nolimits} \left( {{B^\prime }AC} \right),{B^\prime }I \bot AC}\end{array}} \right.\)
Ta có: \(BI = \frac{{AC}}{2} = a\)
\({B^\prime }B = \sqrt {{{(3a)}^2} - {{(a\sqrt 2 )}^2}} = \sqrt 7 a\)
Xét \(\Delta B{B^\prime }I\) vuông tại \(B:\tan \widehat {{B^\prime }IB} = \frac{{{B^\prime }B}}{{BI}} = \frac{{\sqrt 7 a}}{a} = \sqrt 7 \Rightarrow \widehat {{B^\prime }IB} \approx {69,3^^\circ }\)
Câu 3
a) Hai biến cố \(A\) và \(B\) không độc lập
b) \(P(AB) = \frac{3}{{17}}\)
c) \(P(A\bar B) = \frac{{60}}{{119}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \({2^{30}} < {3^{20}}\).
B. \({0,99^\pi } > {0,99^e}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
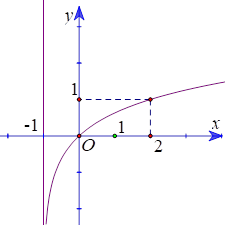
A. \[y = {\log _2}x + 1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.