Vi khuẩn E.coli sống chủ yếu ở đường ruột và có số lượng lớn nhất trong hệ vi sinh vật của cơ thể . Một quần thể vi khuẩn E. coli được quan sát trong điều kiện thích hợp, có tốc độ sinh trưởng được cho bởi hàm số \[f\left( t \right) = {480.2^t}\ln 2.\] Trong đó \[t\] tính bằng giờ \[\left( {t > 0} \right)\], \[f\left( t \right)\] tính bằng cá thể/giờ (Nguồn: R Larson and B.Edwards,Calculus 10e, Cengage). Biết tại thời điểm bắt đầu quan sát, số lượng cá thể được ước tính một cách chính xác khoảng 480 cá thể. Hàm số biểu thị số lượng cá thể theo thời gian \[t\] là:
A. \[F\left( t \right) = {480.2^t} + \ln 2\].
B. \[F\left( t \right) = {480.2^t}\].
C. \[F\left( t \right) = 480.\frac{{{2^t}}}{{\ln 2}}\].
D. \[F\left( t \right) = 480.\frac{{{2^t}}}{{\ln 2}} + C\].
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Do \[\int {f\left( t \right)dt} = \int {{{480.2}^t}\ln 2{\rm{ }}dt} = 480.\ln 2.\frac{{{2^t}}}{{\ln 2}} + C = {480.2^t} + C = F(t)\].
Biết tại thời điểm bắt đầu quan sát, số lượng cá thể được ước tính một cách chính xác khoảng 480 cá thể nên
\[F(0) = {480.2^0} + C = 480 \Rightarrow C = 0\]. Suy ra \[F\left( t \right) = {480.2^t}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 4
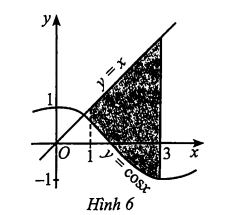
Hình phẳng đã cho được giới hạn bởi các đồ thị hàm số \(y = \cos x,\,y = x\) và hai đường thẳng \(x = 1,\,x = 3\). Khi đó diện tích hình phẳng được tính theo công thức
\(S = \int\limits_1^3 {\left| {\cos x - x} \right|{\rm{d}}x} \). Vì \(x \ge \cos x,\,\forall x \in \left[ {1;3} \right]\) nên ta có:
\(S = \int\limits_1^3 {\left( {x - \cos x} \right){\rm{d}}x} = \left. {\left( {\frac{{{x^2}}}{2} - \sin x} \right)} \right|_1^3 = 4 - \sin 3 + \sin 1 \approx 4\).
Câu 2
A. \[S = \int\limits_{ - 1}^{ - 0,5} {f\left( x \right)dx} \].
B. \[S = \int\limits_{ - 1}^0 {f\left( x \right)dx} \].
C. \[S = - \left| {\int\limits_1^{ - 0,5} {f\left( x \right)dx} } \right|\].
D.\[S = - \int\limits_{ - 1}^{0,5} {f\left( x \right)dx} \].
Lời giải
Đáp án đúng là: D
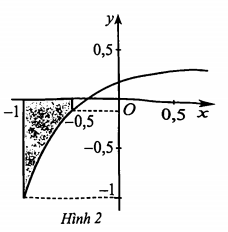
Ta có \[S = \int\limits_{ - 1}^{0,5} {\left| {f\left( x \right)} \right|dx} = - \int\limits_{ - 1}^{0,5} {f\left( x \right)dx} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) Xác suất để một máy bay đến đúng giờ biết rằng nó đã khởi hành đúng giờ là 0,94.
Đúng
Sai
b) Xác suất để một máy bay khởi hành đúng giờ biết rằng nó sẽ đến đúng giờ là 0,85.
Đúng
Sai
c) Xác suất để một máy bay đến đúng giờ biết rằng nó khởi hành không đúng giờ là 0,24.
Đúng
Sai
d) Xác suất để một máy bay khởi hành đúng giờ biết rằng nó sẽ đến không đúng giờ là 0,95.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) Mặt cầu tâm \(I\) đi qua điểm \(M\) có bán kính là \(R = IM = \sqrt 3 \).
Đúng
Sai
b) Phương trình mặt cầu tâm \(I\) và đi qua điểm \(M\) có phương trình là \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 9\).
Đúng
Sai
c) Phương trình mặt phẳng tiếp xúc với mặt cầu tại điểm \(M\) là \( - 2x + 2y - z = 0\).
Đúng
Sai
d) Phương trình mặt cầu tâm \(I\), cắt trục \(Ox\) tại hai điểm \(A\) và \(B\) sao cho độ dài đoạn \(AB = 2\sqrt 3 \) là \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 3} \right)^2} = 16\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \({F_1}(x) = {15^x}\).
B. \({F_2}(x) = {15^x}\ln 15\).
C. \({F_3}(x) = \frac{{{{15}^x}}}{{\log 15}}\).
D. \({F_4}(x) = \frac{{{{15}^x}}}{{\ln 15}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập