Bạn Hải nhận thiết kế logo hình con mắt (phần được tô đậm) cho một cơ sở y tế: Logo là hình phẳng giới hạn bởi hai parabol \[y = f\left( x \right)\] và \[y = g\left( x \right)\] như hình bên dưới (đơn vị trên mỗi trục toạ độ là decimét). Bạn Hải cần tính diện tích của logo để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện tích của logo là bao nhiêu decimét vuông (làm tròn kết quả đến hàng phần mười).
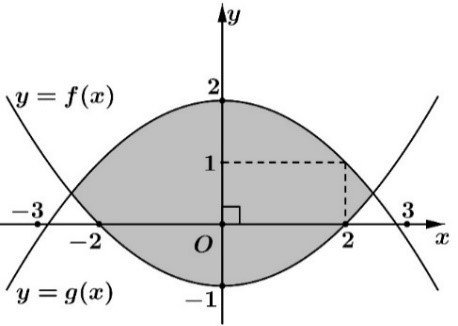
Bạn Hải nhận thiết kế logo hình con mắt (phần được tô đậm) cho một cơ sở y tế: Logo là hình phẳng giới hạn bởi hai parabol \[y = f\left( x \right)\] và \[y = g\left( x \right)\] như hình bên dưới (đơn vị trên mỗi trục toạ độ là decimét). Bạn Hải cần tính diện tích của logo để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện tích của logo là bao nhiêu decimét vuông (làm tròn kết quả đến hàng phần mười).

Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 12 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
Trả lời: 9,8
Gọi parabol \(y = f\left( x \right)\) có dạng \(f\left( x \right) = a{x^2} + bx + c\). Parabol \(y = f\left( x \right)\) nhận \(Oy\) làm trục đối xứng nên ta có \(\frac{{ - b}}{{2a}} = 0 \Leftrightarrow b = 0\). Lại có đồ thị hàm số \(y = f\left( x \right)\) đi qua điểm \(\left( {0; - 1} \right)\) và điểm \(\left( {2;0} \right)\) nên \(a = \frac{1}{4}\) và \(c = - 1\).
Vậy parabol \(y = f\left( x \right) = \frac{1}{4}{x^2} - 1\).
Tương tự, ta cũng có parabol \(y = g\left( x \right) = - \frac{1}{4}{x^2} + 2\).
Phương trình hoành độ giao điểm của \(f\left( x \right)\) và \(g\left( x \right)\) là:
\(\frac{1}{4}{x^2} - 1 = - \frac{1}{4}{x^2} + 2 \Leftrightarrow x = \sqrt 6 \) hoặc \(x = - \sqrt 6 \).
Khi đó, diện tích của logo là:
\[\begin{array}{l}S = \int\limits_{ - \sqrt 6 }^{\sqrt 6 } {\left[ {\left( { - \frac{1}{4}{x^2} + 2} \right) - \left( {\frac{1}{4}{x^2} - 1} \right)} \right]dx} \\\,\,\, = \int\limits_{ - \sqrt 6 }^{\sqrt 6 } {\left( {3 - \frac{1}{2}{x^2}} \right)dx = } \left. {\left( {3x - \frac{{{x^3}}}{6}} \right)} \right|_{ - \sqrt 6 }^{\sqrt 6 } = 4\sqrt 6 \approx 9,8\left( {{\rm{d}}{{\rm{m}}^{\rm{2}}}} \right)\end{array}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 4
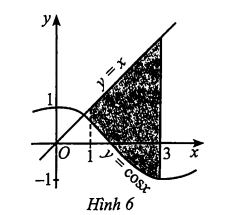
Hình phẳng đã cho được giới hạn bởi các đồ thị hàm số \(y = \cos x,\,y = x\) và hai đường thẳng \(x = 1,\,x = 3\). Khi đó diện tích hình phẳng được tính theo công thức
\(S = \int\limits_1^3 {\left| {\cos x - x} \right|{\rm{d}}x} \). Vì \(x \ge \cos x,\,\forall x \in \left[ {1;3} \right]\) nên ta có:
\(S = \int\limits_1^3 {\left( {x - \cos x} \right){\rm{d}}x} = \left. {\left( {\frac{{{x^2}}}{2} - \sin x} \right)} \right|_1^3 = 4 - \sin 3 + \sin 1 \approx 4\).
Câu 2
Lời giải
Đáp án đúng là: B
Do \[\int {f\left( t \right)dt} = \int {{{480.2}^t}\ln 2{\rm{ }}dt} = 480.\ln 2.\frac{{{2^t}}}{{\ln 2}} + C = {480.2^t} + C = F(t)\].
Biết tại thời điểm bắt đầu quan sát, số lượng cá thể được ước tính một cách chính xác khoảng 480 cá thể nên
\[F(0) = {480.2^0} + C = 480 \Rightarrow C = 0\]. Suy ra \[F\left( t \right) = {480.2^t}\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.