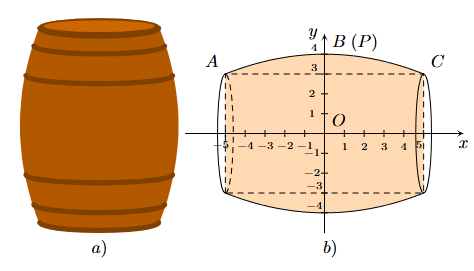
Một thùng rượu vang có dạng khối tròn xoay với bán kính mặt đáy và mặt ở trên là 33 cm, bán kính mặt cắt ở chính giữa thùng là 43 cm. Chiều cao của thùng rượu là 112 cm, bao gồm phần thân thùng rượu, hai đế đỡ thùng rượu (mỗi đế cao 3 cm) và thùng rượu được ghép từ các thanh gỗ sồi với độ dày mỗi thanh gỗ là 3 cm (Hình a). Hình b mô phỏng phần bên trong thùng rượu có dạng một khối tròn xoay tạo thành khi quay một phần của parabol \(\left( P \right):y = a{x^2} + bx + c\) quanh trục hoành (mỗi đơn vị ứng với với 10 cm).

Thùng đó chứa được tối đa bao nhiêu lít rượu? (kết quả làm tròn đến hàng đơn vị).

Trả lời: 0

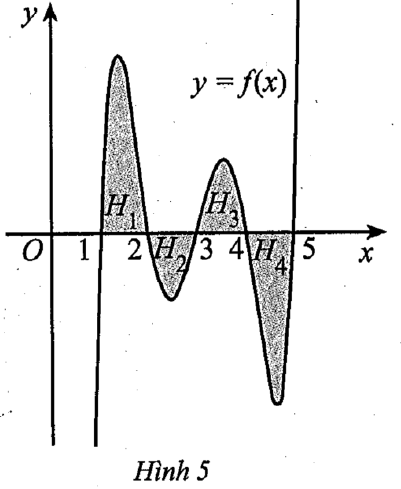
Ta có: \(\int\limits_1^5 {f\left( x \right)} {\rm{d}}x = \int\limits_1^2 {f\left( x \right)} {\rm{d}}x + \int\limits_2^3 {f\left( x \right)} {\rm{d}}x + \int\limits_3^4 {f\left( x \right)} {\rm{d}}x + \int\limits_4^5 {f\left( x \right)} {\rm{d}}x\)

\( = \int\limits_1^2 {\left| {f\left( x \right)} \right|} {\rm{d}}x - \int\limits_2^3 {\left| {f\left( x \right)} \right|} {\rm{d}}x + \int\limits_3^4 {\left| {f\left( x \right)} \right|} {\rm{d}}x - \int\limits_4^5 {\left| {f\left( x \right)} \right|} {\rm{d}}x\)

\( = {S_{{H_1}}} - {S_{{H_2}}} + {S_{{H_3}}} - {S_{{H_4}}} = \frac{9}{4} - \frac{{11}}{{12}} + \frac{{11}}{{12}} - \frac{9}{4} = 0\).

Đáp án đúng là: D

Ta có \(\int\limits_1^2 {\left( {f\left( x \right) + g\left( x \right)} \right)dx = 2} \)\( \Leftrightarrow \int\limits_1^2 {f\left( x \right)dx + \int\limits_1^2 {g\left( x \right)dx} } = 2\)

\( \Leftrightarrow - 1 + \int\limits_1^2 {g\left( x \right)dx} = 2 \Leftrightarrow \int\limits_1^2 {g\left( x \right)dx} = 3\).