PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Một vật chuyển động với gia tốc \(a\left( t \right) = \frac{1}{{{t^2} + 3t + 2}}\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\), trong đó \(t\) là khoảng thời gian tính từ thời điểm ban đầu. Vận tốc chuyển động của vật là \(v\left( t \right)\), vận tốc ban đầu của vật là \({v_0} = 3\ln 2\left( {{\rm{m/s}}} \right).\)

a) Đ, b) S, c) S, d) Đ

a) Đường thẳng \({d_1}\) có vectơ chỉ phương là \(\overrightarrow {{u_1}} = \left( {1; - 1;1} \right)\).

b) Ta có \(\overrightarrow {{u_2}} = \left( {3;3; - 1} \right)\) là một vectơ chỉ phương của đường thẳng \({d_2}\).

Mặt phẳng đi qua điểm \(A\left( {1; - 1;3} \right)\) và vuông góc với đường thẳng \({d_2}\) nhận vectơ \(\overrightarrow {{u_2}} = \left( {3;3; - 1} \right)\) làm vectơ pháp tuyến có phương trình là \(3\left( {x - 1} \right) + 3\left( {y + 1} \right) - \left( {z - 3} \right) = 0\)\( \Leftrightarrow 3x + 3y - z + 3 = 0\).

c) Giả sử \(d \cap {d_1} = M\). Khi đó \(M\left( {2 + t; - 1 - t;1 + t} \right)\).

Đường thẳng \(d\) nhận \(\overrightarrow {AM} = \left( {1 + t; - t;t - 2} \right)\) làm vectơ chỉ phương.

Lại có \(d \bot {d_2}\) nên \(\overrightarrow {AM} .\overrightarrow {{u_2}} = 0 \Leftrightarrow \left( {1 + t} \right).3 + \left( { - t} \right).3 + \left( {t - 2} \right).\left( { - 1} \right) = 0\)\( \Leftrightarrow t = 5\).

Suy ra \(\overrightarrow {AM} = \left( {6; - 5;3} \right)\).

d) Đường thẳng \(d\) đi qua điểm \(A\left( {1; - 1;3} \right)\) và có một vectơ chỉ phương \(\overrightarrow {AM} = \left( {6; - 5;3} \right)\) có phương trình là \(\frac{{x - 1}}{6} = \frac{{y + 1}}{{ - 5}} = \frac{{z - 3}}{3}\).

Thay tọa độ điểm \(K\left( {13; - 11;9} \right)\) vào phương trình đường thẳng d ta được

\(\frac{{13 - 1}}{6} = \frac{{ - 11 + 1}}{{ - 5}} = \frac{{9 - 3}}{3}\) (đúng). Do đó đường thẳng \(d\) đi qua điểm \(K\left( {13; - 11;9} \right)\).

Trả lời: 1008

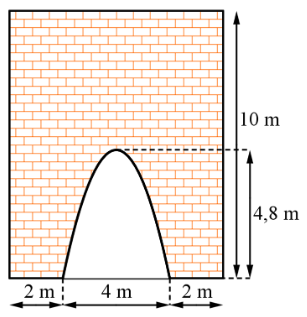
Ta có diện tích bức tường hình chữ nhật là \(10.8 = 80\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Chọn hệ trục tọa độ \(Oxy\) sao cho gốc \(O\) trùng với chân bên trái cổng parabol như hình sau:

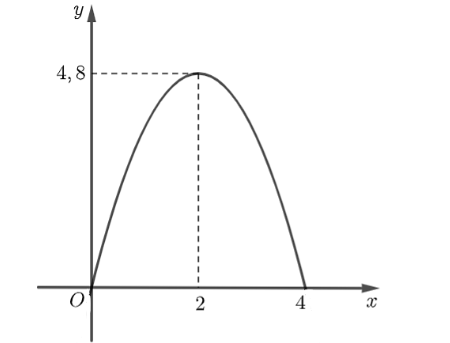
Giả sử \(P:y = a{x^2} + bx + c\).

Vì \(\left( P \right)\) đi qua \(\left( {0;0} \right),\left( {2;4,8} \right),\left( {4;0} \right)\) nên ta có \(\left\{ \begin{array}{l}4a + 2b + c = 4,8\\16a + 4b + c = 0\\c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{6}{5}\\b = \frac{{24}}{5}\\c = 0\end{array} \right.\).

Do đó \(\left( P \right):y = - \frac{6}{5}{x^2} + \frac{{24}}{5}x\).

Diện tích của chiếc cổng là: \(S = \int\limits_0^4 {\left| { - \frac{6}{5}{x^2} + \frac{{24}}{5}x} \right|dx} = \frac{{64}}{5}\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Suy ra diện tích cần sơn là: \(80 - \frac{{64}}{5} = 67,2\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Chi phí cần để sơn là: \(67,2.15000 = 100800\) đồng = 1008 nghìn đồng.