Cho tam giác ABC có ba góc đều nhọn, BH là đường cao kẻ từ B (\(H \in AC)\). Gọi D, E lần lượt là trung điểm của AB và AC, F là điểm đối xứng của điểm H qua DE.
a. Chứng minh rằng tứ giác ABFH nội tiếp.
b. Chứng minh \(\widehat {FBA} = \widehat {EFH}.\)
Chứng minh rằng BF đi qua tâm đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC có ba góc đều nhọn, BH là đường cao kẻ từ B (\(H \in AC)\). Gọi D, E lần lượt là trung điểm của AB và AC, F là điểm đối xứng của điểm H qua DE.
a. Chứng minh rằng tứ giác ABFH nội tiếp.
b. Chứng minh \(\widehat {FBA} = \widehat {EFH}.\)
Chứng minh rằng BF đi qua tâm đường tròn ngoại tiếp tam giác ABC.Quảng cáo
Trả lời:
Giải bởi Vietjack
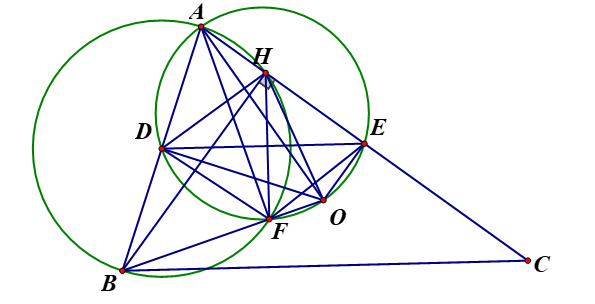
a) Xét \(\Delta AHB\) vuông cân tại H có D là trung điểm \(AB \Rightarrow DA = DB = DH\) (1).
Vì F là điểm đối xứng của điểm H qua DE nên \(DH = DF\) (2).
Từ (1) và (2) \( \Rightarrow DA = DH = DB = DF\).
Suy ra bốn điểm A, H, B, F cùng thuộc được tròn đường kính AB.
Vậy tứ giác ABFH nội tiếp.
b) Tứ giác ABFH nội tiếp (câu 6a) \( \Rightarrow \widehat {FBA} = \widehat {FHE}\) (3).
Vì F là điểm đối xứng của điểm H qua DE nên \(EH = EF.\)
Suy ra \(\Delta EHF\) cân tại E \( \Rightarrow \widehat {FHE} = \widehat {EFH}\) (4).
Từ (3), (4) \( \Rightarrow \widehat {FBA} = \widehat {EFH}.\)
c) Vì F là điểm đối xứng của điểm H qua DE nên
\(\widehat {FDE} = \frac{1}{2}\widehat {HDF}\;\;\;\;\;\left( 5 \right)\)
Từ câu 6a, có A, H, B, F thuộc đường tròn tâm D đường kính AB nên
\(\widehat {HAF} = \frac{1}{2}\widehat {HDF}\;\;\;\left( 6 \right)\).
Từ (5), (6) \( \Rightarrow \widehat {FDE} = \widehat {HAF} = \widehat {EAF}.\)
Suy ra tứ giác FDAE nội tiếp. (7)
Xét đường tròn (O) tâm O ngoại tiếp \(\Delta ABC\) có
D là trung điểm dây AB \( \Rightarrow \widehat {ODA} = {90^0}\)
E là trung điểm dây AC \( \Rightarrow \widehat {OEA} = {90^0}\)
Xét tứ giác ODAE có:
\(\widehat {ODA} + \widehat {OEA} = {180^0}\)
Nên tứ giác ODAE nội tiếp đường tròn đường kính AO. (8)
Kết hợp (7), (8) \( \Rightarrow A,D,\;F,\;O,\;E\) cùng thuộc đường tròn đường kính AO.
\( \Rightarrow \widehat {AFO} = \widehat {ADO} = {90^0}\) (cùng chắn cung AO).
Mặt khác: \(\widehat {AFB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn đường kính AB)
Suy ra: \(\widehat {AFO} + \widehat {AFB} = {180^0}\), nghĩa là B, F, O thẳng hàng.
Vậy BF đi qua tâm đường tròn ngoại tiếp \(\Delta ABC.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ký hiệu các điểm như hình minh họa bên.
Trong đó:
A, B, M, N, H là các tiếp điểm giữa dây đai với các ống thép.
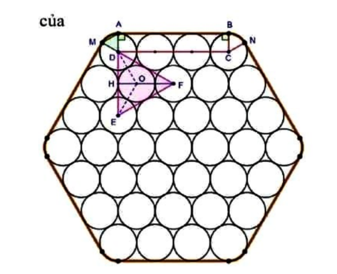
D, C, E, F, O là tâm của một số ống thép.
Giả sử các ống thép tiếp xúc khít nhau và dây đai buộc chính xác.
Dễ thấy ABCD là hình chữ nhật.
\( \Rightarrow AB = CD = 3d = 3.10 = 30\;\left( {cm} \right)\;\;\left( 1 \right)\)
Nên hiển hiên các điểm A, D, H, E thẳng hàng.
Xét \(\Delta DEF\) có:
\(DE = 2DH = 2\sqrt {O{D^2} - O{H^2}} = 2\sqrt {{{\left( {2r} \right)}^2} - {r^2}} = 2\sqrt {3r} = 10\sqrt 3 \;\left( {cm} \right)\)
Tương tự cũng tính được \(DF = 10\sqrt 3 \;\left( {cm} \right)\) và \(EF = 10\sqrt 3 \;\left( {cm} \right).\)
Như vậy \(DE = EF = DF = 10\sqrt 3 \;\left( {cm} \right)\) nên \(\Delta DEF\) là tam giác đều \( \Rightarrow \widehat {EDF} = {60^0}.\)
Suy ra \(\widehat {ADM} = \widehat {EDF} = {60^0}\) (đối đỉnh).
Chiều dài cung AM bằng
\(\frac{{\pi .5.60}}{{180}} = \frac{5}{3}\pi \;\;\left( {cm} \right)\;\;\;\;\left( 2 \right)\)
Từ hình vẽ, kết hợp (1) và (2) ta tính được chiều dài dây đai là:
\(l = 6.\frac{5}{3}\pi + 6.30 = 180 + 10\pi \;\left( {cm} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \({x^2} + ax + b = 0\) (1).
Không mất tính tổng quát, giả sử \({x_1} = 5 + \sqrt {21} \) và \({x_2}\) là nghiệm còn lại.
Thay \(x = {x_1} = 5 + \sqrt {21} \) vào (1) ta được:
\({\left( {5 + \sqrt {21} } \right)^2} + a\left( {5 + \sqrt {21} } \right) + b = 0\)
\( \Leftrightarrow 46 + 10\sqrt {21} + 5a + \sqrt {21} a + b = 0\)
\( \Leftrightarrow \left( {a + 10} \right)\sqrt {21} + \left( {5a + b + 46} \right) = 0\)
Vì a; b là các số nguyên nên ta có hệ:
\(\left\{ {\begin{array}{*{20}{c}}{a + 10 = 0}\\{5a + b + 46 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 10}\\{b = - 46 - 5a}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - 10}\\{b = 4}\end{array}} \right.} \right.} \right.\)
Suy ra phương trình (1) là \({x^2} - 10x = 4 = 0.\)
Theo hệ thức Vi-ét, ta được:
\({x_1} + {x_2} = 10 \Rightarrow \left( {5 + \sqrt {21} } \right) + {x_2} = 10 \Rightarrow {x_2} = 5 - \sqrt {21} \).
Vậy nghiệm còn lại là \(x = 5 - \sqrt {21} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập