Cho phương trình \[{x^2} + 2(m + 1)x + {m^2} + 2m - 3 = 0\,\](\(m\)là tham số). Tìm \(m\) để phương trình có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn:\(x_1^2 + x_2^2 = 16.\)
Quảng cáo
Trả lời:
Khi đó: \(x_1^2 + x_2^2 = 16\)
\(\)\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}.{x_2} = 16\\ \Leftrightarrow {\left[ { - 2\left( {m + 1} \right)} \right]^2} - 2\left( {{m^2} + 2m - 3} \right) = 16\\ \Leftrightarrow 4{m^2} + 8m + 4 - 2{m^2} - 4m + 6 = 16\\ \Leftrightarrow 2{m^2} + 4m - 6 = 0\end{array}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Đến ngày 02/09/2023 số tiền có được trong tài khoản tiết kiệm là: \(2.005.000\left( {1 + 0,005} \right) + 1.000.000 = 3.015.025\)(VNĐ) |
|
Đến ngày 02/10/2023 số tiền có được trong tài khoản tiết kiệm là: \(1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + 1,{{005}^3}} \right] \simeq 4.030.100\)(VNĐ) |
|
Sau kỳ gởi tháng thứ \(n\) số tiền được tính theo công thức \({T_n} = 1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + \cdots + 1,{{005}^n}} \right]\) |
|
Vào ngày 02/7/2026 bạn Tuấn đã tiết kiệm được 3 năm (36 tháng). \({T_{36}} = 1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + \cdots + 1,{{005}^{36}}} \right]\) |
|
Suy ra \(1,005{T_{36}} = 1.000.000\left[ {1,005 + 1,{{005}^2} + \cdots + 1,{{005}^{36}} + 1,{{005}^{37}}} \right]\) |
|
\[1,005{T_{36}} - {T_{36}} = 1.000.000\left[ {1,{{005}^{37}} - 1} \right]\] \[ \Rightarrow {T_{36}} = \frac{{1.000.000\left[ {1,{{005}^{37}} - 1} \right]}}{{0,005}} \approx 40.532.785\,\](VNĐ) |
Lời giải
|
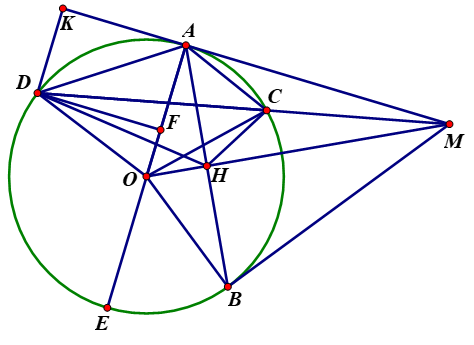
Xét \(\Delta MAC\) và \(\Delta MDA\) có \(\widehat {AMD}\) chung |
|
\(\widehat {MAC} = \widehat {MDA}\) (Cùng chắn ) |
|
Suy ra (g-g) |
|
\( \Rightarrow \frac{{MA}}{{MD}} = \frac{{MC}}{{MA}} \Rightarrow M{A^2} = MC.MD\) |
|
Ta có: \(\widehat {OAM} = {90^0}\)(tính chất của tiếp tuyến) \(MA = MB\)(tính chất hai tiếp tuyến cắt nhau) và \(OA = OB\) \( \Rightarrow OM\)là trung trực \(AB\) hay \(OM \bot AB\) tại \(H\) \( \Rightarrow A{M^2} = MH.MO\)(hệ thức lượng trong tam giác vuông) |
|
\( \Rightarrow MH.MO = MC.MD\,\left( { = M{A^2}} \right)\) |
|
\(\frac{{MH}}{{MC}} = \frac{{MD}}{{MO}}\) và \(\widehat {DMO}\) chung (c-g-c) |
|
\( \Rightarrow \widehat {MDH} = \widehat {MOC}\) (hai góc tương ứng) hay \(\widehat {CDH} = \widehat {HOC}\) \( \Rightarrow \) tứ giác \(DOHC\) nội tiếp đường tròn |
|
Dựng đường cao \(DK\) của \(\Delta MAD\). Khi đó \({S_{\Delta MAD}} = \frac{1}{2}MA.DK\) |
|
\({S_{\Delta MAD}} = \frac{1}{2}MA.DK\) đạt giá trị lớn nhất khi và chỉ khi \(DK\)lớn nhất (\(MA\) không đổi) |
|
Gọi \(E\) là điểm đối xứng với \(A\) qua \(O\). Qua \(D\) dựng đường thẳng song song \(MA\) cắt \(AE\) tại \(F \Rightarrow DK = AF\) |
|
Khi \(D\) di chuyển trên cung lớn \(AB\) thì \(F\) di chuyển trên đường kính \(AE\). Suy ra \(AF\) lớn nhất khi \(AF\) là đường kính hay \(D \equiv F \equiv E\) |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.