Bạn Tuấn lập kế hoạch tiết kiệm tiền để mua một cái laptop phục vụ cho việc học tập như sau: Hằng tháng, Tuấn tiết kiệm các khoản chi tiêu cá nhân để dành ra một triệu đồng. Vào ngày 01 hằng tháng Tuấn gửi vào tài khoản tiết kiệm của mình một triệu đồng và bắt đầu gửi vào ngày 01 tháng 7 năm 2023 để hưởng lãi suất 0,5%/tháng theo hình thức lãi kép (nghĩa là tiền lãi của tháng trước được cộng vào vốn để tính lãi cho tháng sau) và duy trì việc này liên tục trong 3 năm. (Biết tài khoản ban đầu của Tuấn là 0 đồng và hàng tháng Tuấn không rút vốn, lãi).
a)Tính số tiền tiết kiệm Tuấn có được trong tài khoản tính đến ngày 02/8/2023.
b)Hãy đề xuất công thức tính tổng số tiền trong tài khoản tiết kiệm sau kỳ gửi tháng thứ \(n\)(\(n\)là số tự nhiên, \(n \ge 3\)). Sử dụng công thức đó để tính số tiền Tuấn có được trong tài khoản tính đến ngày 02/7/2026.
a)Tính số tiền tiết kiệm Tuấn có được trong tài khoản tính đến ngày 02/8/2023.
b)Hãy đề xuất công thức tính tổng số tiền trong tài khoản tiết kiệm sau kỳ gửi tháng thứ \(n\)(\(n\)là số tự nhiên, \(n \ge 3\)). Sử dụng công thức đó để tính số tiền Tuấn có được trong tài khoản tính đến ngày 02/7/2026.
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Đến ngày 02/09/2023 số tiền có được trong tài khoản tiết kiệm là: \(2.005.000\left( {1 + 0,005} \right) + 1.000.000 = 3.015.025\)(VNĐ) |
|
Đến ngày 02/10/2023 số tiền có được trong tài khoản tiết kiệm là: \(1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + 1,{{005}^3}} \right] \simeq 4.030.100\)(VNĐ) |
|
Sau kỳ gởi tháng thứ \(n\) số tiền được tính theo công thức \({T_n} = 1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + \cdots + 1,{{005}^n}} \right]\) |
|
Vào ngày 02/7/2026 bạn Tuấn đã tiết kiệm được 3 năm (36 tháng). \({T_{36}} = 1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + \cdots + 1,{{005}^{36}}} \right]\) |
|
Suy ra \(1,005{T_{36}} = 1.000.000\left[ {1,005 + 1,{{005}^2} + \cdots + 1,{{005}^{36}} + 1,{{005}^{37}}} \right]\) |
|
\[1,005{T_{36}} - {T_{36}} = 1.000.000\left[ {1,{{005}^{37}} - 1} \right]\] \[ \Rightarrow {T_{36}} = \frac{{1.000.000\left[ {1,{{005}^{37}} - 1} \right]}}{{0,005}} \approx 40.532.785\,\](VNĐ) |
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
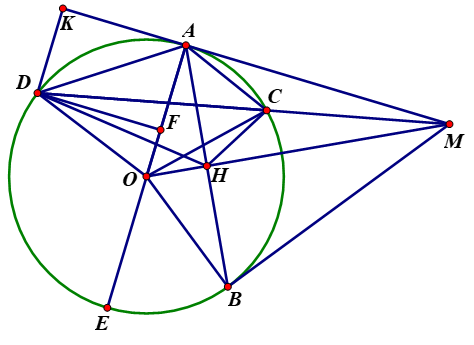
Xét \(\Delta MAC\) và \(\Delta MDA\) có \(\widehat {AMD}\) chung |
|
\(\widehat {MAC} = \widehat {MDA}\) (Cùng chắn ) |
|
Suy ra (g-g) |
|
\( \Rightarrow \frac{{MA}}{{MD}} = \frac{{MC}}{{MA}} \Rightarrow M{A^2} = MC.MD\) |
|
Ta có: \(\widehat {OAM} = {90^0}\)(tính chất của tiếp tuyến) \(MA = MB\)(tính chất hai tiếp tuyến cắt nhau) và \(OA = OB\) \( \Rightarrow OM\)là trung trực \(AB\) hay \(OM \bot AB\) tại \(H\) \( \Rightarrow A{M^2} = MH.MO\)(hệ thức lượng trong tam giác vuông) |
|
\( \Rightarrow MH.MO = MC.MD\,\left( { = M{A^2}} \right)\) |
|
\(\frac{{MH}}{{MC}} = \frac{{MD}}{{MO}}\) và \(\widehat {DMO}\) chung (c-g-c) |
|
\( \Rightarrow \widehat {MDH} = \widehat {MOC}\) (hai góc tương ứng) hay \(\widehat {CDH} = \widehat {HOC}\) \( \Rightarrow \) tứ giác \(DOHC\) nội tiếp đường tròn |
|
Dựng đường cao \(DK\) của \(\Delta MAD\). Khi đó \({S_{\Delta MAD}} = \frac{1}{2}MA.DK\) |
|
\({S_{\Delta MAD}} = \frac{1}{2}MA.DK\) đạt giá trị lớn nhất khi và chỉ khi \(DK\)lớn nhất (\(MA\) không đổi) |
|
Gọi \(E\) là điểm đối xứng với \(A\) qua \(O\). Qua \(D\) dựng đường thẳng song song \(MA\) cắt \(AE\) tại \(F \Rightarrow DK = AF\) |
|
Khi \(D\) di chuyển trên cung lớn \(AB\) thì \(F\) di chuyển trên đường kính \(AE\). Suy ra \(AF\) lớn nhất khi \(AF\) là đường kính hay \(D \equiv F \equiv E\) |
Lời giải
Với điều kiện \(x > 0,\,\,x \ne 4\) ta có:
\(P = \left( {\frac{2}{{\sqrt x - 2}} - \frac{{\sqrt x - 2}}{{\sqrt x + 2}}} \right):\frac{{x\sqrt x }}{{x - 4}} = \frac{{2(\sqrt x + 2) - {{(\sqrt x - 2)}^2}}}{{x - 4}}:\frac{{x\sqrt x }}{{x - 4}}\)
\(\)\[ = \frac{{2\sqrt x + 4 - x + 4\sqrt x - 4}}{{x - 4}}.\frac{{x - 4}}{{x\sqrt x }} = \frac{{6\sqrt x - x}}{{x\sqrt x }}\]
\[ = \frac{{6 - \sqrt x }}{x}\]
\(P = \frac{1}{3} \Leftrightarrow \frac{{6 - \sqrt x }}{x} = \frac{1}{3} \Leftrightarrow x + 3\sqrt x - 18 = 0 \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 3\\\sqrt x = - \,6\,(L)\end{array} \right. \Leftrightarrow x = 9\,(TM)\). \(\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập