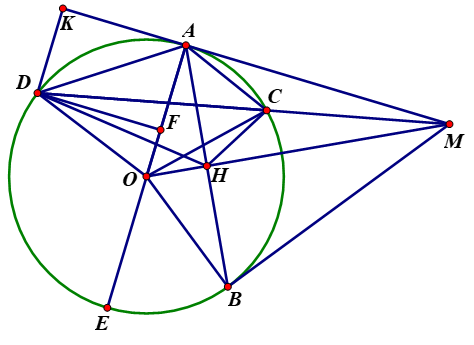
Từ điểm\(M\)nằm ngoài đường tròn \((O),\)kẻ hai tiếp tuyến \(MA,\,\,MB\) (\(A,\,\,B\) là tiếp điểm), cát tuyến \(MCD\) không đi qua tâm \(O,\)\(MD > MC\).
a) Chứng minh rằng \(M{A^2} = MC.MD.\)
b)Gọi \(H\) là giao điểm của \(MO\) và \(AB\). Chứng minh rằng tứ giác \(CHOD\) nội tiếp
c) Tìm vị trí của \(D\) để tam giác \(MAD\) có diện tích lớn nhất
b)Gọi \(H\) là giao điểm của \(MO\) và \(AB\). Chứng minh rằng tứ giác \(CHOD\) nội tiếp
c) Tìm vị trí của \(D\) để tam giác \(MAD\) có diện tích lớn nhất
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Xét \(\Delta MAC\) và \(\Delta MDA\) có \(\widehat {AMD}\) chung |
|
\(\widehat {MAC} = \widehat {MDA}\) (Cùng chắn ) |
|
Suy ra (g-g) |
|
\( \Rightarrow \frac{{MA}}{{MD}} = \frac{{MC}}{{MA}} \Rightarrow M{A^2} = MC.MD\) |
|
Ta có: \(\widehat {OAM} = {90^0}\)(tính chất của tiếp tuyến) \(MA = MB\)(tính chất hai tiếp tuyến cắt nhau) và \(OA = OB\) \( \Rightarrow OM\)là trung trực \(AB\) hay \(OM \bot AB\) tại \(H\) \( \Rightarrow A{M^2} = MH.MO\)(hệ thức lượng trong tam giác vuông) |
|
\( \Rightarrow MH.MO = MC.MD\,\left( { = M{A^2}} \right)\) |
|
\(\frac{{MH}}{{MC}} = \frac{{MD}}{{MO}}\) và \(\widehat {DMO}\) chung (c-g-c) |
|
\( \Rightarrow \widehat {MDH} = \widehat {MOC}\) (hai góc tương ứng) hay \(\widehat {CDH} = \widehat {HOC}\) \( \Rightarrow \) tứ giác \(DOHC\) nội tiếp đường tròn |
|
Dựng đường cao \(DK\) của \(\Delta MAD\). Khi đó \({S_{\Delta MAD}} = \frac{1}{2}MA.DK\) |
|
\({S_{\Delta MAD}} = \frac{1}{2}MA.DK\) đạt giá trị lớn nhất khi và chỉ khi \(DK\)lớn nhất (\(MA\) không đổi) |
|
Gọi \(E\) là điểm đối xứng với \(A\) qua \(O\). Qua \(D\) dựng đường thẳng song song \(MA\) cắt \(AE\) tại \(F \Rightarrow DK = AF\) |
|
Khi \(D\) di chuyển trên cung lớn \(AB\) thì \(F\) di chuyển trên đường kính \(AE\). Suy ra \(AF\) lớn nhất khi \(AF\) là đường kính hay \(D \equiv F \equiv E\) |
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Đến ngày 02/09/2023 số tiền có được trong tài khoản tiết kiệm là: \(2.005.000\left( {1 + 0,005} \right) + 1.000.000 = 3.015.025\)(VNĐ) |
|
Đến ngày 02/10/2023 số tiền có được trong tài khoản tiết kiệm là: \(1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + 1,{{005}^3}} \right] \simeq 4.030.100\)(VNĐ) |
|
Sau kỳ gởi tháng thứ \(n\) số tiền được tính theo công thức \({T_n} = 1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + \cdots + 1,{{005}^n}} \right]\) |
|
Vào ngày 02/7/2026 bạn Tuấn đã tiết kiệm được 3 năm (36 tháng). \({T_{36}} = 1.000.000\left[ {1 + 1,005 + 1,{{005}^2} + \cdots + 1,{{005}^{36}}} \right]\) |
|
Suy ra \(1,005{T_{36}} = 1.000.000\left[ {1,005 + 1,{{005}^2} + \cdots + 1,{{005}^{36}} + 1,{{005}^{37}}} \right]\) |
|
\[1,005{T_{36}} - {T_{36}} = 1.000.000\left[ {1,{{005}^{37}} - 1} \right]\] \[ \Rightarrow {T_{36}} = \frac{{1.000.000\left[ {1,{{005}^{37}} - 1} \right]}}{{0,005}} \approx 40.532.785\,\](VNĐ) |
Lời giải
Với điều kiện \(x > 0,\,\,x \ne 4\) ta có:
\(P = \left( {\frac{2}{{\sqrt x - 2}} - \frac{{\sqrt x - 2}}{{\sqrt x + 2}}} \right):\frac{{x\sqrt x }}{{x - 4}} = \frac{{2(\sqrt x + 2) - {{(\sqrt x - 2)}^2}}}{{x - 4}}:\frac{{x\sqrt x }}{{x - 4}}\)
\(\)\[ = \frac{{2\sqrt x + 4 - x + 4\sqrt x - 4}}{{x - 4}}.\frac{{x - 4}}{{x\sqrt x }} = \frac{{6\sqrt x - x}}{{x\sqrt x }}\]
\[ = \frac{{6 - \sqrt x }}{x}\]
\(P = \frac{1}{3} \Leftrightarrow \frac{{6 - \sqrt x }}{x} = \frac{1}{3} \Leftrightarrow x + 3\sqrt x - 18 = 0 \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 3\\\sqrt x = - \,6\,(L)\end{array} \right. \Leftrightarrow x = 9\,(TM)\). \(\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập