Cho đoạn thẳng \(AB\) và \(C\)là điểm nằm trên đoạn \(AB\) sao cho \(BC > AC\). Trên cùng một nửa mặt phẳng bờ là đường thẳng \(AB\), vẽ nửa đường tròn đường kính \(AB\) và nửa đường tròn đường kính \(BC\). Lấy điểm \(M\) thuộc nửa đường tròn đường kính \(BC\) (\(M \ne B\), \(M \ne C\)). Kẻ \(MH\) vuông góc với \(BC\)\(\left( {H \in BC} \right)\), đường thẳng \(MH\) cắt nửa đường tròn đường kính \(AB\) tại \(K\). Hai đường thẳng \(AK\) và \(CM\) cắt nhau tại \(E\).
a) Chứng minh tứ giác \(BMKE\) nội tiếp và \(B{E^2} = BA \cdot BC\).
b) Từ \(C\) kẻ \(CN\) vuông góc với \(AB\) (\(N\)thuộc nửa đường tròn đường kính \(AB\)), gọi \(P\) là giao điểm của \(NK\)và \(CE\). Chứng minh rằng tâm đường tròn nội tiếp của các tam giác \(BNE\) và \(PNE\) cùng nằm trên đường thẳng \(BP\).
Cho đoạn thẳng \(AB\) và \(C\)là điểm nằm trên đoạn \(AB\) sao cho \(BC > AC\). Trên cùng một nửa mặt phẳng bờ là đường thẳng \(AB\), vẽ nửa đường tròn đường kính \(AB\) và nửa đường tròn đường kính \(BC\). Lấy điểm \(M\) thuộc nửa đường tròn đường kính \(BC\) (\(M \ne B\), \(M \ne C\)). Kẻ \(MH\) vuông góc với \(BC\)\(\left( {H \in BC} \right)\), đường thẳng \(MH\) cắt nửa đường tròn đường kính \(AB\) tại \(K\). Hai đường thẳng \(AK\) và \(CM\) cắt nhau tại \(E\).
a) Chứng minh tứ giác \(BMKE\) nội tiếp và \(B{E^2} = BA \cdot BC\).
b) Từ \(C\) kẻ \(CN\) vuông góc với \(AB\) (\(N\)thuộc nửa đường tròn đường kính \(AB\)), gọi \(P\) là giao điểm của \(NK\)và \(CE\). Chứng minh rằng tâm đường tròn nội tiếp của các tam giác \(BNE\) và \(PNE\) cùng nằm trên đường thẳng \(BP\).Quảng cáo
Trả lời:
Giải bởi Vietjack
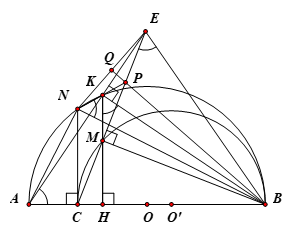
a) Ta có: \(\widehat {BME} = \widehat {BKE} = {90^ \circ }\) nên tứ giác \(BMKE\) nội tiếp.
\( \Rightarrow \widehat {HKB} = \widehat {CEB}\)
mà \(\widehat {HKB} = \widehat {BAE}\) (cùng phụ với \(\widehat {HKA}\))
\( \Rightarrow \widehat {BAE} = \widehat {CEB}\).
\(\Delta BEC\) đồng dạng với \(\Delta BAE\) (vì \(\widehat {ABE}\) chung và \(\widehat {BAE} = \widehat {CEB}\))
Do đó \(\frac{{BE}}{{AB}} = \frac{{BC}}{{BE}} \Rightarrow B{E^2} = BC \cdot AB\).b) Xét tam giác vuông \(ABN\)có \(CN \bot AB \Rightarrow B{N^2} = BC \cdot AB\)
mà \(B{E^2} = BC \cdot AB\) suy ra \(BN = BE\) hay \(\Delta BNE\) cân tại \(B\), suy ra \(\widehat {BNE} = \widehat {BEN}\). \(\left( 1 \right)\)
Mặt khác, theo câu trên ta có \(\widehat {CEB} = \widehat {BAE}\) và \(\widehat {BAE} = \widehat {BNP}\) suy ra \(\widehat {CEB} = \widehat {BNP}\). (2)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {PNE} = \widehat {PEN}\) hay \(\Delta PNE\) cân tại \(P\) \( \Rightarrow NP = PE\).
Vì \(NP = PE\) và \(BN = BE\) nên \(BP \bot NE\).
Suy ra \(BP\) là đường phân giác của các góc \(\widehat {EBN}\) và \(\widehat {EPN}\).
Do đó tâm đường tròn nội tiếp các tam giác \(BNE\) và \(PNE\) cùng nằm trên đường thẳng \(BP\).Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
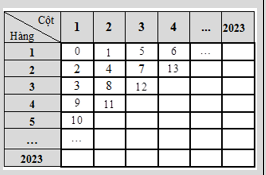
Theo quy luật: Đánh số thứ tự các đường chéo như số thứ tự các hàng - Đường chéo thứ nhất viết 1 số (số \(0\)) - Đường chéo thứ hai viết 2 số (từ 1 đến 2) ... - Đường chéo thứ \(n\) viết \(n\) số. |
|
Vậy với \(n\) đường chéo đầu tiên ta đã viết được \(1 + 2 + \cdots + n = \frac{{n\left( {n + 1} \right)}}{2}\) số (bắt đầu từ số \(0\))
Lại có \(2016 = \frac{{63 \cdot 64}}{2} < 2024 < \frac{{64 \cdot 65}}{2} = 2080\). Do đó với \(63\) đường chéo ta đã viết được \(2016\)số từ \(0\)đến \(2015\).
Vậy các số tiếp theo \(2016,{\rm{ }}\)\(2017,{\rm{ }}\)\(2018,{\rm{ }}\)\(2019,{\rm{ }}\)\(2020,{\rm{ }}\)\(2021,{\rm{ }}\)\(2022,\)\(2023,{\rm{ }}2024\) sẽ được viết ở đường chéo thứ \(64\).
Kể từ đường chéo thứ hai, tính từ trái qua phải, từ dưới lên trên, ta thấy đường chéo mang số lẻ thì tăng dần, đường chéo mang số chẵn thì giảm dần. Vậy số 2016 thì ở đầu cột 64, hàng 1.
Vậy số 2024 được viết ở cột 56, hàng 9.
b) Chứng minh được bất đẳng thức \(\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}.\)
Ta có \(\frac{1}{{2a + b + c}} = \frac{1}{4} \cdot \frac{4}{{\left( {a + b} \right) + \left( {a + c} \right)}} \le \frac{1}{4}\left( {\frac{1}{{a + b}} + \frac{1}{{a + c}}} \right)\)
\( \Rightarrow \frac{{bc}}{{2a + b + c}} \le \frac{1}{4}\left( {\frac{{bc}}{{a + b}} + \frac{{bc}}{{a + c}}} \right)\) (1)
Tương tự, ta có
\(\frac{{ac}}{{2b + a + c}} \le \frac{1}{4}\left( {\frac{{ac}}{{b + c}} + \frac{{ac}}{{b + a}}} \right)\) (2)
\(\frac{{ab}}{{2c + a + b}} \le \frac{1}{4}\left( {\frac{{ab}}{{a + c}} + \frac{{ab}}{{b + c}}} \right)\). (3)
Cộng (1), (2) và (3) vế theo vế ta được
Dấu "=" xảy ra \( \Leftrightarrow a = b = c.\)
Lời giải
\[\left\{ \begin{array}{l}2{x^2} + {y^2} - 3xy + 7x - 5y + 6 = 0 & & (1)\\4{x^2} - {y^2} + 9x + 9 = \sqrt {2x + y + 2} + \sqrt {x + 4y + 1} & (2)\end{array} \right.\]
Điều kiện: \(\left\{ \begin{array}{l}2x + y + 2 \ge 0\\x + 4y + 1 \ge 0.\end{array} \right.\)
Xét phương trình \(\left( 1 \right)\): \[2{x^2} + {y^2} - 3xy + 7x - 5y + 6 = 0\]
\( \Leftrightarrow 2{x^2} + \left( {7 - 3y} \right)x + {y^2} - 5y + 6 = 0\) (*)
Ta xem (*) là phương trình bậc hai theo biến \(x\). Biệt thức
Phương trình (*) có hai nghiệm
\(\left[ \begin{array}{l}x = \frac{{3y - 7 + y - 1}}{4} = y - 2\\x = \frac{{3y - 7 - \left( {y - 1} \right)}}{4} = \frac{{y - 3}}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}y = x + 2\\y = 2x + 3.\end{array} \right.\)
+) Với \(y = x + 2\), thay vào phương trình \(\left( 2 \right)\) ta được:
\(3{x^2} + 5x + 5 = \sqrt {3x + 4} + \sqrt {5x + 9} \)
\( \Leftrightarrow 3{x^2} + 3x + \left[ {\left( {x + 2} \right) - \sqrt {3x + 4} } \right] + \left[ {\left( {x + 3} \right) - \sqrt {5x + 9} } \right] = 0\)
\( \Leftrightarrow 3\left( {{x^2} + x} \right) + \frac{{{x^2} + x}}{{x + 2 + \sqrt {3x + 4} }} + \frac{{{x^2} + x}}{{x + 3 + \sqrt {5x + 9} }} = 0\)
\( \Leftrightarrow x\left( {x + 1} \right)\left[ {3 + \frac{1}{{x + 2 + \sqrt {3x + 4} }} + \frac{1}{{x + 3 + \sqrt {5x - 9} }}} \right] = 0\) (**)
Với điều kiện \(\left\{ \begin{array}{l}3x + 4 \ge 0\\5x + 9 \ge 0\end{array} \right. \Leftrightarrow x \ge - \frac{4}{3}\), ta có
\(3 + \frac{1}{{x + 2 + \sqrt {3x + 4} }} + \frac{1}{{x + 3 + \sqrt {5x - 9} }} > 0\)
Do đó \(\left( {**} \right) \Leftrightarrow \left[ \begin{array}{l}x = 0 & \Rightarrow y = 2\\x = - 1 & \Rightarrow y = 1.\end{array} \right.\)
+) Với \(y = 2x + 3\), thay vào phương trình \(\left( 2 \right)\) ta được
\(\sqrt {4x + 5} + \sqrt {9x + 13} + 3x = 0\)
\( \Leftrightarrow \left( {\sqrt {4x + 5} - 1} \right) + \left( {\sqrt {9x + 13} - 2} \right) + 3x + 3 = 0\)
\( \Leftrightarrow \frac{{4\left( {x + 1} \right)}}{{\sqrt {4x + 5} + 1}} + \frac{{9\left( {x + 1} \right)}}{{\sqrt {9x + 13} + 2}} + 3\left( {x + 1} \right) = 0\)
\( \Leftrightarrow \left( {x + 1} \right)\left[ {\frac{4}{{\sqrt {4x + 5} + 1}} + \frac{9}{{\sqrt {9x + 13} + 2}} + 3} \right] = 0\) (***)
Với điều kiện \(\left\{ \begin{array}{l}4x + 5 \ge 0\\9x + 13 \ge 0\end{array} \right. \Leftrightarrow x \ge - \frac{5}{4}\), ta có
\(\frac{4}{{\sqrt {4x + 5} + 1}} + \frac{9}{{\sqrt {9x + 13} + 2}} + 3 > 0\).
Do đó \(\left( {***} \right) \Leftrightarrow x + 1 = 0 \Leftrightarrow x = - 1 \Rightarrow y = 1.\)
Vậy hệ phương trình đã cho có hai nghiệm \(\left( {x;y} \right) = \left\{ {\left( {0;2} \right),\left( { - 1;1} \right)} \right\}\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập