1. Giải phương trình 3x3 – 7x2 + 6x + 4 = 3\(\sqrt[3]{{\frac{{16{x^2} + 6x + 2}}{3}}}\) .
2. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{{x^2} + {y^2} + x + y = 8\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\{2{x^2} + {y^2} - 3xy + 3x - 2y + 1 = 0}\end{array}} \right.\)
1. Giải phương trình 3x3 – 7x2 + 6x + 4 = 3\(\sqrt[3]{{\frac{{16{x^2} + 6x + 2}}{3}}}\) .
2. Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{{x^2} + {y^2} + x + y = 8\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\{2{x^2} + {y^2} - 3xy + 3x - 2y + 1 = 0}\end{array}} \right.\)
Quảng cáo
Trả lời:
1.
ĐKXĐ: \(\forall \)x Î R
3x3 – 7x2 + 6x + 4 = 3\(\sqrt[3]{{\frac{{16{x^2} + 6x + 2}}{3}}}\)
3x3 + 9x2 + 12x + 6 = 16x2 + 6x + 2 + 3\(\sqrt[3]{{\frac{{16{x^2} + 6x + 2}}{3}}}\)
Đặt \(\sqrt[3]{{\frac{{16{x^2} + 6x + 2}}{3}}}\) = t , ta có:
3x3 + 9x2 + 12x + 6 = 3t3 + 3t
x3 + 3x2 + 4x + 2 = t3 + t
(x + 1)3 + (x + 1) = t3 + t
(x + 1 – t) [(x + 1)2 – (x + 1)t + t2 +1] = 0
Mà (x + 1)2 – (x + 1)t + t2 +1 > 0 Þ x + 1 – t = 0
x + 1 = t
x + 1 = \(\sqrt[3]{{\frac{{16{x^2} + 6x + 2}}{3}}}\)
3x3 + 9x2 + 12x + 6 = 16x2 + 6x + 2
3x3 – 7x2 + 3x + 1 = 0
3x3 – 3x2 – 4x2 + 4x – x + 1 = 0
(x – 1)( 3x2 – 4x + 1) = 0
\(\left[ {\begin{array}{*{20}{c}}{x = 1\;\;\;\;\;}\\{x = \frac{{2 + \sqrt 7 }}{3}}\\{x = \frac{{2 - \sqrt 7 }}{3}}\end{array}} \right.\)
Thử lại thấy cả 3 nghiệm thoả mãn.
Vậy x \(\left\{ {1;\;\frac{{2 + \sqrt 7 }}{3};\;\frac{{2 - \sqrt 7 }}{3}\;} \right\}\)
\(\begin{array}{l}2.\left\{ \begin{array}{l}{x^2} + {y^2} + x + y = 8\left( 1 \right)\\2{x^2} + {y^2} - 3xy + 3x - 2y + 1 = 0\left( 2 \right)\end{array} \right.\\\left( 2 \right) \Leftrightarrow 2{x^2} + 3\left( {1 - y} \right)x + {\left( {y - 1} \right)^2} = 0 \Leftrightarrow \left( {x + 1 - y} \right)\left( {2x + 1 - y} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}x = \frac{{y - 1}}{2}\\x = y - 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}y = 2x + 1 \Rightarrow \left( 1 \right) \Leftrightarrow {x^2} + {\left( {2x + 1} \right)^2} + x + 2x + 1 = 8 \Leftrightarrow \left[ \begin{array}{l}x = - 2 \Rightarrow y = - 3\\x = \frac{3}{5} \Rightarrow y = \frac{{11}}{5}\end{array} \right.\\y = x + 1 \Rightarrow \left( 1 \right) \Leftrightarrow {x^2} + {\left( {x + 1} \right)^2} + x + x + 1 = 8 \Leftrightarrow 2{x^2} + 4x - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1;y = 2\\x = - 3;y = - 2\end{array} \right.\end{array} \right.\\(x;y) \in \left\{ {\left( { - 2; - 3} \right);\left( {\frac{3}{5};\frac{{11}}{5}} \right);\left( {1;2} \right);\left( { - 3; - 2} \right)} \right\}\end{array}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Theo bài ra, ta có: a, b, c > 0 và ab + bc + ca = 3abc Û \(\frac{1}{a}\) + \(\frac{1}{b}\) + \(\frac{1}{c}\) = 3
Đặt \(\frac{1}{a}\) là x; \(\frac{1}{b}\) là y; \(\frac{1}{c}\) là z (x, y, z > 0; x + y + z = 3)
Suy ra: \(\sqrt {\frac{a}{{3{b^2}{c^2} + abc}}} \) + \(\sqrt {\frac{{\frac{1}{x}}}{{\frac{3}{{{y^2}{z^2}}}\; + \frac{1}{{xyz}}}}} \) + \(\sqrt {\frac{{{y^2}{z^2}}}{{x\left( {x + y + z} \right) + yz}}} \) = \(\sqrt {\frac{{{y^2}{z^2}}}{{3x + xy}}} \)
Suy ra: T £ \(\frac{1}{2}\left( {\frac{{yz + zx}}{{x + y}} + \frac{{yz + yx}}{{x + z}} + \frac{{xy + zx}}{{y + z}}} \right)\) = \(\frac{1}{2}\) (x + y + z) = \(\frac{3}{2}\)
Dấu “=” xảy ra Û a = b = c = 1
Lời giải
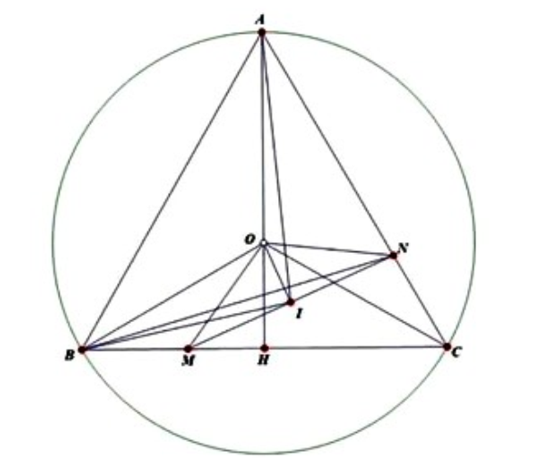
a) Xét \(\Delta \)OBM và \(\Delta \)OCM có:
\(\left. {\begin{array}{*{20}{c}}{BM = CN\;\;\;\;\;\;\;\;\;\;\;\;}\\{\angle CBM = \angle OCN}\\{OB = OC\;\;\;\;\;\;\;\;\;\;\;\;\;}\end{array}} \right\}\) Þ \(\Delta \)OBM ~ \(\Delta \)OCM (c.g.c)
Þ OM = ON hay O nằm trên đường trung trực MN
Þ OI \( \bot \) MN
Xét tứ giác OIHM có:\(\;\angle OIM = \angle OHM = 90^\circ \)
=> OIHM nội tiếp hay 4 điểm O, M, H, I cùng thuộc 1 đường tròn.
b) Chứng minh được IH // AB. Từ đó suy ra đường cao hạ từ I và từ H cùng vuông góc với AB có độ dài bằng nhau. Do đó, diện tích tam giác IAB luôn bằng diện tích tam giác AHB không đổi
Theo chứng minh câu a) có OI \( \bot \) MN và \(\angle MON = 90^\circ \) nên
MN = 2MI = 2.OM.sin60\(^\circ \) = OM\(\sqrt 3 \)
Khi M chuyển động trên BH thì OM ³ OH với dấu đẳng thức xảy ra khi và chỉ khi M trùng H. Từ đó suy ra:
min MN = OH\(\sqrt 3 \)
đạt được khi và chỉ khi M trùng H.
2.
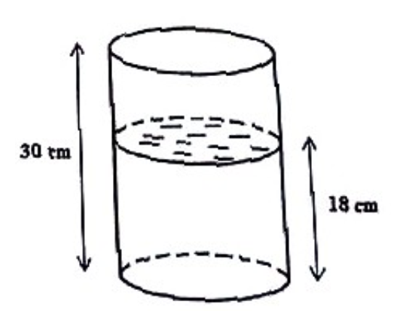
Diện tích đáy bình bằng \(\frac{1}{6}\) diện tích xung quanh Þ pr2 = \(\frac{1}{6}\).2prh Þ h = 3r
Ta có: h = 30 Þ r = 10
Thể tích nước cần đổ thêm để vừa đầy bình là: V = pr2.(h – 18) = 3,14.102.12 = 3768(cm3)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.