(2,0 điểm) Cho hai biểu thức và .
a) Tìm điều kiện xác định của biểu thức \(A\) và \(B.\)
(2,0 điểm) Cho hai biểu thức và .
a) Tìm điều kiện xác định của biểu thức \(A\) và \(B.\)
Quảng cáo
Trả lời:
Hướng dẫn giải
a) – Xét biểu thức \(A = \frac{{\sqrt x + 2}}{{\sqrt x - 4}}\).
Điều kiện xác định của biểu thức \(A\) và \(x \ge 0\) và \(\sqrt x - 4 \ne 0\) hay \(x \ge 0,\,\,x \ne 16.\)
– Xét biểu thức \[B = \frac{{\sqrt x - 2}}{{\sqrt x + 4}} - \frac{{10\sqrt x - 8}}{{16 - x}}\].
Với \(x \ge 0\), ta có:
⦁ \[16 - x = \left( {4 + \sqrt x } \right)\left( {4 - \sqrt x } \right) = - \left( {\sqrt x + 4} \right)\left( {\sqrt x - 4} \right)\].
⦁ \(x \ge 0\) nên \(\sqrt x \ge 0,\) suy ra \(\sqrt x + 4 > 0.\)
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0\) và \(\sqrt x - 4 \ne 0\) hay \(x \ge 0,\,\,x \ne 16.\)
Vậy điều kiện xác định của biểu thức \(A\) và biểu thức \(B\) đều là \(x \ge 0,\,\,x \ne 16.\)
Câu hỏi cùng đoạn
Câu 2:
b) Tính giá trị của biểu thức \(A\) khi \(x = 4 - 2\sqrt 3 .\)
b) Tính giá trị của biểu thức \(A\) khi \(x = 4 - 2\sqrt 3 .\)
b) Tính giá trị của biểu thức \(A\) khi \(x = 4 - 2\sqrt 3 .\)
Vì \(x = 4 - 2\sqrt 3 = 3 - 2\sqrt 3 + 1\) nên \(x = {\left( {\sqrt 3 - 1} \right)^2}\) và \(\sqrt x = \sqrt 3 - 1\).
Thay vào \(A\) ta được \(A = \frac{{\sqrt 3 - 1 + 2}}{{\sqrt 3 - 1 - 4}} = \frac{{\sqrt 3 + 1}}{{\sqrt 3 - 5}}\)\( = \frac{{\left( {\sqrt 3 + 1} \right)\left( {\sqrt 3 + 5} \right)}}{{ - 2}}\)\( = - 4 - 3\sqrt 3 \).
Vậy khi \(x = 4 - 2\sqrt 3 \) thì \(A = - 4 - 3\sqrt 3 \).
Câu 3:
c) Chứng minh rằng \(B = \frac{{\sqrt x }}{{\sqrt x - 4}}.\)
c) Chứng minh rằng \(B = \frac{{\sqrt x }}{{\sqrt x - 4}}.\)
c) Với \(x \ge 0\,,\,\,x \ne 16\,,\) ta có:
\[B = \frac{{\sqrt x - 2}}{{\sqrt x + 4}} - \frac{{10\sqrt x - 8}}{{16 - x}}\]
\[ = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 4} \right)}}{{\left( {\sqrt x + 4} \right)\left( {\sqrt x - 4} \right)}} + \frac{{10\sqrt x - 8}}{{\left( {\sqrt x + 4} \right)\left( {\sqrt x - 4} \right)}}\]
\[ = \frac{{x - 6\sqrt x + 8 + 10\sqrt x - 8}}{{\left( {\sqrt x + 4} \right)\left( {\sqrt x - 4} \right)}}\]
\[ = \frac{{x + 4\sqrt x }}{{\left( {\sqrt x + 4} \right)\left( {\sqrt x - 4} \right)}}\]\[ = \frac{{\sqrt x }}{{\sqrt x - 4}}\].
Câu 4:
d) Tìm \(m\) để phương trình \(\frac{A}{B} = m\) có nghiệm.
d) Tìm \(m\) để phương trình \(\frac{A}{B} = m\) có nghiệm.
d) Ta có \(\frac{A}{B} = \frac{{\sqrt x + 2}}{{\sqrt x - 4}}:\frac{{\sqrt x }}{{\sqrt x - 4}}\) \( = \frac{{\sqrt x + 2}}{{\sqrt x - 4}}.\frac{{\sqrt x - 4}}{{\sqrt x }}\)\( = \frac{{\sqrt x + 2}}{{\sqrt x }}\).
Phương trình \(\frac{A}{B} = m\) trở thành \(\frac{{\sqrt x + 2}}{{\sqrt x }} = m\) hay \(\sqrt x + 2 = m\sqrt x \).
Suy ra \(\left( {m - 1} \right)\sqrt x = 2\).
Để phương trình có nghiệm ta cần có \(m - 1 > 0\) hay \(m > 1\), đồng thời \(\frac{2}{{m - 1}} \ne 16\) hay \(m \ne \frac{9}{8}\).
Vậy, với \(m > 1\) và \(m \ne \frac{9}{8}\) thì phương trình \(\frac{A}{B} = m\) có nghiệm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) \[\frac{x}{{x + 3}} - \frac{2}{{x - 3}} = \frac{{ - 2x - 6}}{{{x^2} - 9}}\]
\[\frac{{x\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} - \frac{{2\left( {x + 3} \right)}}{{\left( {x + 3} \right)\left( {x - 3} \right)}} = \frac{{ - 2x - 6}}{{\left( {x + 3} \right)\left( {x - 3} \right)}}\]
\[x\left( {x - 3} \right) - 2\left( {x + 3} \right) = - 2x - 6\]
\[{x^2} - 5x - 6 = - 2x - 6\]
\[{x^2} - 3x = 0\]
\(x\left( {x - 3} \right) = 0\)
\(x = 0\) hoặc \(x - 3 = 0\)
\(x = 0\) (thỏa mãn) hoặc \(x = 3\) (không thỏa mãn).
Vậy phương trình đã cho có nghiệm là \(x = 0.\)Lời giải
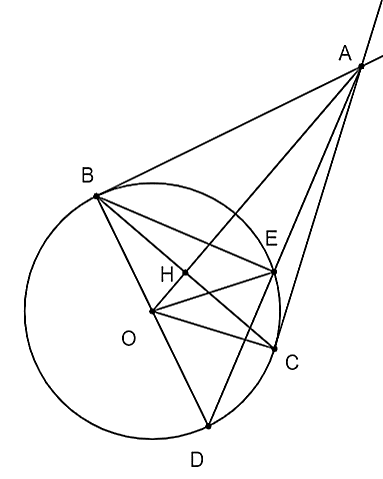
a) Xét đường tròn \[\left( O \right)\] có: \[AB,AC\] lần lượt là tiếp tuyến tại \[B,C\] nên \[AB = AC\] (tính chất hai tiếp tuyến cắt nhau) .
Suy ra \[A\] thuộc đường trung trực của \[BC\].
Mà \[OB = OC = R\] nên \[O\] thuộc đường trung trực của \[BC\]
Do đó \[OA\] là đường trung trực của \[BC\] nên \[OA \bot BC\] tại \[H\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.