(3,5 điểm)
1. Giải các phương trình, bất phương trình sau:
a) \(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{{x^2} - 1}}.\)
(3,5 điểm)
1. Giải các phương trình, bất phương trình sau:
a) \(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{{x^2} - 1}}.\)Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Điều kiện xác định: \(x \ne 1\) và \(x \ne - 1\).
Ta có: \(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{{x^2} - 1}}\)
\(\frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} - \frac{{{{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{8}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\(\frac{{{{\left( {x - 1} \right)}^2} - {{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{8}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\({\left( {x - 1} \right)^2} - {\left( {x + 1} \right)^2} = 8\)
\(\left( {x - 1 + x + 1} \right)\left( {x - 1 - x - 1} \right) = 8\)
\(2x.\left( { - 2} \right) = 8\)
\( - 4x = 8\)
\(x = - 2\) (thỏa mãn).
Vậy nghiệm của phương trình là \(x = - 2\).Câu hỏi cùng đoạn
Câu 2:
1. Giải các phương trình, bất phương trình sau:
b) \(0,5x + 7\left( {x - 2} \right) \le \frac{1}{2}x - 1.\)
Giải bởi Vietjack
b) \(0,5x + 7\left( {x - 2} \right) \le \frac{1}{2}x - 1\)
\(0,5x + 7x - 14 \le 0,5x - 1\)
\(0,5x + 7x - 0,5x \le 14 - 1\)
\(7x \le 13\)
\(x \le \frac{{13}}{7}\).
Vậy nghiệm của bất phương trình là \(x \le \frac{{13}}{7}\).Câu 3:
1. Giải các phương trình, bất phương trình sau:
c) \(\sqrt {18x + 9} - \sqrt {8x + 4} + \frac{1}{3}\sqrt {2x + 1} = 4.\)
Giải bởi Vietjack
c) \(\sqrt {18x + 9} - \sqrt {8x + 4} + \frac{1}{3}\sqrt {2x + 1} = 4\) (ĐKXĐ: \(x \ge - \frac{1}{2})\)
\(\sqrt {9\left( {2x + 1} \right)} - \sqrt {4\left( {2x + 1} \right)} + \frac{1}{3}\sqrt {2x + 1} = 4\)
\(3\sqrt {2x + 1} - 2\sqrt {2x + 1} + \frac{1}{3}\sqrt {2x + 1} = 4\)
\(\frac{4}{3}\sqrt {2x + 1} = 4\)
\(\sqrt {2x + 1} = 3\)
\(2x + 1 = 9\)
\(2x = 8\)
\(x = 4\) (thỏa mãn)
Vậy phương trình có nghiệm là \(x = 4\).
Câu 4:
2. Một tổ may gồm 47 công nhân cả nam và nữ được giao nhiệm vụ may 350 chiếc áo cho cổ động viên để cổ vũ đội tuyển U23 Việt Nam tại SEA GAME 31. Để hoàn thành nhiệm vụ, mỗi công nhân nam may 8 chiếc áo, mỗi công nhân nữ may 7 chiếc áo. Tính số công nhân nam và số công nhân nữ của tổ may đó.
2. Một tổ may gồm 47 công nhân cả nam và nữ được giao nhiệm vụ may 350 chiếc áo cho cổ động viên để cổ vũ đội tuyển U23 Việt Nam tại SEA GAME 31. Để hoàn thành nhiệm vụ, mỗi công nhân nam may 8 chiếc áo, mỗi công nhân nữ may 7 chiếc áo. Tính số công nhân nam và số công nhân nữ của tổ may đó.
Giải bởi Vietjack
2. Gọi \[x,y\] (người) lần lượt là số công nhân nam và nữ của tổ may đó \[\left( {x,y \in \mathbb{N}*\,;\,\,x,y < 47} \right)\].
Vì tổ may gồm 47 công nhân nên \[x + y = 47\]. (1)
Vì mỗi công nhân nam may 8 chiếc áo, mỗi công nhân nữ may 7 chiếc áo, may được tổng cộng 350 chiếc áo nên ta có phương trình \[8x + 7y = 350\]. (2)
Từ (1) và (2) ta có hệ phương trình: \[\left\{ \begin{array}{l}x + y = 47\\8x + 7y = 350\end{array} \right.\].
Nhân cả hai vế của phương trình (1) với 7, ta được hệ phương trình mới là: \[\left\{ \begin{array}{l}7x + 7y = 329\\8x + 7y = 350.\end{array} \right.\]
Trừ từng vế của phương trình thứ hai cho phương trình thứ nhất của hệ trên nên \[x = 21\] (thỏa mãn).
Thay \[x = 21\] vào phương trình (1), ta được: \[21 + y = 47\] nên \[y = 26\] (thỏa mãn).
Vậy tổ có 26 công nhân nam và 21 công nhân nữ.
Câu 5:
3. Tổng chi phí của một doanh nghiệp sản xuất áo sơ mi là 40 triệu đồng/tháng. Giá bán của mỗi chiếc áo sơ mi là 350 nghìn đồng. Doanh nghiệp đó cần thu được lợi nhuận ít nhất là 1,38 tỉ đồng sau 1 năm.
a) Viết bất phương trình mô tả tình huống trên.
b) Hỏi trung bình mỗi tháng doanh nghiệp phải bán được ít nhất bao nhiêu chiếc áo sơ mi để đạt được mức lợi nhuận trên?
3. Tổng chi phí của một doanh nghiệp sản xuất áo sơ mi là 40 triệu đồng/tháng. Giá bán của mỗi chiếc áo sơ mi là 350 nghìn đồng. Doanh nghiệp đó cần thu được lợi nhuận ít nhất là 1,38 tỉ đồng sau 1 năm.
a) Viết bất phương trình mô tả tình huống trên.
b) Hỏi trung bình mỗi tháng doanh nghiệp phải bán được ít nhất bao nhiêu chiếc áo sơ mi để đạt được mức lợi nhuận trên?
Giải bởi Vietjack
3. a) Gọi \(x\) là số chiếc áo sơ mi trung bình mỗi tháng doanh nghiệp bán được \[\left( {x \in {\mathbb{N}^ * }} \right)\].
Lợi nhuận của doanh nghiệp sau 12 tháng là:
\[12 \cdot \left( {350\,\,000x - 410\,\,000\,\,000} \right)\] (đồng).
Để doanh nghiệp thu được ít nhất 1,38 tỉ đồng thì:
\[12 \cdot \left( {350\,\,000x - 410\,\,000\,\,000} \right) \ge 1\,\,380\,\,000\,\,000\]
Vậy bất phương trình cần tìm là \[12 \cdot \left( {350\,\,000x - 410\,\,000\,\,000} \right) \ge 1\,\,380\,\,000\,\,000\].
b) Giải bất phương trình
\[12 \cdot \left( {350\,\,000x - 410\,\,000\,\,000} \right) \ge 1\,\,380\,\,000\,\,000\]
\[7x - 8\,\,200 \ge 2\,\,300\]
\[7x \ge 10\,\,500\]
\(x \ge 1\,\,500\).
Mà \(0 \le x \le 25\,,\,\,x \in \mathbb{N}*\) nên người ứng tuyển cần phải trả lời chính xác ít nhất thì mới được dự thi tiếp vòng sau.Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
![a) Chứng minh \[OA \bot BC\] và \[AM \cdot AN = AH \cdot AO = A{O^2} - {R^2}.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/2-1766496288.png)
a) ⦁ Xét đường tròn \[\left( O \right)\] có \[AB,AC\] là hai tiếp cắt nhau tại \[A\] nên \[AB = AC\](tính chất hai tiếp tuyến cắt nhau). Do đó \[A\] thuộc đường trung trực \[BC\].
Mặt khác, \[OB = OC = R\] nên \[O\] thuộc trung trực của đoạn thẳng \[BC\].
Suy ra \(OA\) là đường trung trực của đoạn thẳng \(BC\), do đó \[OA \bot BC\] tại \[H\].
⦁ Vì \(AB\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B\) nên \(AB \bot OB\) tại \(B.\)
Xét \[\Delta HAB\] và \[\Delta BAO\] có: \(\widehat {AHB} = \widehat {ABO} = 90^\circ \) và \(\widehat {OAB}\) là góc chung.
Do đó (g.g)
Suy ra \[\frac{{HA}}{{BA}} = \frac{{AB}}{{AO}}\] hay \[AH \cdot AO = A{B^2}\] (1).
Xét \(\Delta OAB\) vuông tại \(B,\) ta có: \[A{B^2} = A{O^2} - O{B^2} = A{O^2} - {R^2}\] (định lí Pythagore). (2)
Lại có:
\[AM \cdot AN = \left( {AO - OM} \right)\left( {AO + ON} \right)\]
\[ = A{O^2} + AO \cdot ON - OM \cdot AO - OM \cdot ON\]
\[ = A{O^2} - OM \cdot ON\]\[ = A{O^2} - {R^2}\] (vì \(OM = ON = R)\) (3)
Từ (1), (2), (3) suy ra \[AM \cdot AN = AH \cdot AO = A{O^2} - {R^2}.\]
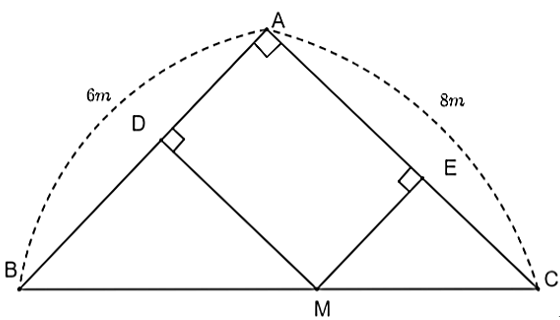
Lời giải
a) – Xét biểu thức \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\).
Điều kiện xác định của biểu thức \(A\) và \(x \ge 0\) và \(\sqrt x - 1 \ne 0\) hay \(x \ge 0,\,\,x \ne 1.\)
– Xét biểu thức \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\).
Với \(x \ge 0\), ta có:
⦁ \(x + \sqrt x = \sqrt x \left( {\sqrt x + 1} \right)\); \(x - \sqrt x = \sqrt x \left( {\sqrt x - 1} \right);\) \(x - 1 = \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right).\)
⦁ \(x \ge 0\) nên \(\sqrt x \ge 0,\) suy ra \(\sqrt x + 1 > 0.\)
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0\) và \(\sqrt x \ne 0,\,\,x - 1 \ne 0\) hay \(x > 0,\,\,x \ne 1.\)
Vậy, điều kiện xác định của biểu thức \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\) là \(x \ge 0,x \ne 1\) và điều kiện xác định của biểu thức \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\) là \(x > 0,x \ne 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập