Bộ 5 đề thi cuối kì 1 Toán 9 Kết nối tri thức (Tự luận) có đáp án - Đề 4
25 người thi tuần này 4.6 478 lượt thi 15 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Đoạn văn 1
Lời giải
a) – Xét biểu thức \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\).
Điều kiện xác định của biểu thức \(A\) và \(x \ge 0\) và \(\sqrt x - 1 \ne 0\) hay \(x \ge 0,\,\,x \ne 1.\)
– Xét biểu thức \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\).
Với \(x \ge 0\), ta có:
⦁ \(x + \sqrt x = \sqrt x \left( {\sqrt x + 1} \right)\); \(x - \sqrt x = \sqrt x \left( {\sqrt x - 1} \right);\) \(x - 1 = \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right).\)
⦁ \(x \ge 0\) nên \(\sqrt x \ge 0,\) suy ra \(\sqrt x + 1 > 0.\)
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0\) và \(\sqrt x \ne 0,\,\,x - 1 \ne 0\) hay \(x > 0,\,\,x \ne 1.\)
Vậy, điều kiện xác định của biểu thức \(A = \frac{{\sqrt x \left( {x + 1} \right)}}{{2\left( {\sqrt x - 1} \right)}}\) là \(x \ge 0,x \ne 1\) và điều kiện xác định của biểu thức \(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\) là \(x > 0,x \ne 1.\)
Lời giải
b) Thay \(x = \frac{1}{9}\) (thỏa mãn điều kiện) vào biểu thức \(A,\) ta được:
\(A = \frac{{\sqrt {\frac{1}{9}} \left( {\frac{1}{9} + 1} \right)}}{{2\left( {\sqrt {\frac{1}{9}} - 1} \right)}} = \frac{{\frac{1}{3}.\frac{{10}}{9}}}{{2\left( {\frac{1}{3} - 1} \right)}} = \frac{{\frac{{10}}{{27}}}}{{ - \frac{4}{3}}} = - \frac{5}{{18}}.\)
Vậy \(A = - \frac{5}{{18}}\) khi \(x = \frac{1}{9}\).
Lời giải
c) Với \(x > 0,x \ne 1\), ta có:
\(B = \frac{1}{{x + \sqrt x }} + \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{x - \sqrt x }}\)
\( = \frac{1}{{\sqrt x \left( {\sqrt x + 1} \right)}} + \frac{{2\sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}}\)
\[ = \frac{{\sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} + \frac{{2\sqrt x \cdot \sqrt x }}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{\sqrt x + 1}}{{\sqrt x \left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\]
\( = \frac{{\sqrt x - 1 + 2x - \sqrt x - 1}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)\( = \frac{{2x - 2}}{{\sqrt x \left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{2\left( {x - 1} \right)}}{{\sqrt x \left( {x - 1} \right)}}\)\( = \frac{2}{{\sqrt x }}\).
Vậy với \(x > 0,x \ne 1\) thì \(B = \frac{2}{{\sqrt x }}\).
Lời giải
d) Với \(x > 1,\) ta có:
Xét \(P = \sqrt x + 1 + \frac{2}{{\sqrt x - 1}} = \sqrt x - 1 + \frac{2}{{\sqrt x - 1}} + 2\) với \(x > 1.\)
Do \(x > 1\) nên \(\sqrt x - 1 > 0\).
Áp dụng bất đẳng thức Cauchy, ta có:
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} \ge 2\sqrt {\left( {\sqrt x - 1} \right).\frac{2}{{\sqrt x - 1}}} \)
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} \ge 2\sqrt 2 \)
\(\sqrt x - 1 + \frac{2}{{\sqrt x - 1}} + 2 \ge 2\sqrt 2 + 2\)
Suy ra \(P \ge 2\sqrt 2 + 2\) với \(x > 1\).
Dấu “=” xảy ra khi và chỉ khi \(\sqrt x - 1 = \frac{2}{{\sqrt x - 1}}\) .
Giải phương trình:
\(\sqrt x - 1 = \frac{2}{{\sqrt x - 1}}\)
\({\left( {\sqrt x - 1} \right)^2} = 2\)
\(\sqrt x - 1 = \sqrt 2 \) (do \(\sqrt x - 1 > 0)\)
\(\sqrt x = \sqrt 2 + 1\)
\(x = 3 + 2\sqrt 2 \) (thỏa mãn).
Vậy giá trị nhỏ nhất của \(P = 2\sqrt 2 + 2\) khi \(x = 3 + 2\sqrt 2 \).
Đoạn văn 2
(3,5 điểm)
Lời giải
a) Điều kiện xác định: \(x \ne 1\) và \(x \ne - 1\).
Ta có: \(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{{x^2} - 1}}\)
\(\frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} - \frac{{{{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{8}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\(\frac{{{{\left( {x - 1} \right)}^2} - {{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{8}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\({\left( {x - 1} \right)^2} - {\left( {x + 1} \right)^2} = 8\)
\(\left( {x - 1 + x + 1} \right)\left( {x - 1 - x - 1} \right) = 8\)
\(2x.\left( { - 2} \right) = 8\)
\( - 4x = 8\)
\(x = - 2\) (thỏa mãn).
Vậy nghiệm của phương trình là \(x = - 2\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
(1,5 điểm) Sau một trận bão lớn, một cái cây mọc thẳng đứng ở vị trí \(C\) đã bị gãy ngang tại \(A\) (như hình vẽ). Ngọn cây chạm mặt đất cách gốc một khoảng \(BC = 5{\rm{ m}}\). Biết rằng phần ngọn bị gãy \(AB\) và phần gốc \(AC\) có tỉ lệ \(3:2\).
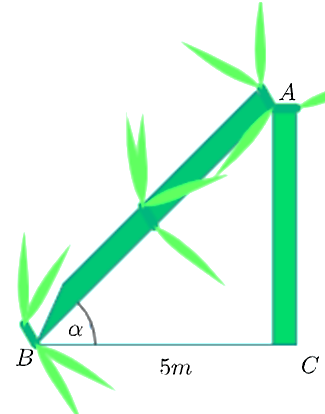
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
(2,5 điểm) Cho đường tròn \[\left( {O;R} \right)\] và một điểm \[A\] nằm ngoài đường tròn \[\left( O \right)\]. Từ \[A\] vẽ hai tiếp tuyến \[AB,AC\] của đường tròn \[\left( O \right)\] (\[B,\,\,C\] là hai tiếp điểm). Gọi \[H\] là giao điểm của \[OA\] và \[BC.\] Tia \[AO\] cắt đường tròn \[\left( O \right)\] tại \[M,N\] (\[M\] nằm giữa \[A\] và \[N\]).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.