Bộ 5 đề thi cuối kì 1 Toán 9 Kết nối tri thức (Tự luận) có đáp án - Đề 3
23 người thi tuần này 4.6 478 lượt thi 15 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Đoạn văn 1
(2,0 điểm) Cho hai biểu thức: và .
Lời giải
a) ⦁ Xét biểu thức \(A = \frac{{\sqrt x + 2}}{{\sqrt x - 2}} - \frac{{\sqrt x - 2}}{{\sqrt x + 2}} + \frac{{4x}}{{x - 4}}\).
Điều kiện xác định của biểu thức \(A\) là \(x \ge 0,\,\,\sqrt x - 2 \ne 0,\,\,\sqrt x + 2 \ne 0,\,\,x - 4 \ne 0.\)
Với \(x \ge 0\), ta có: \(\sqrt x - 2 \ne 0\) khi \(x \ne 4;\)
\(\sqrt x + 2 > 0\);
\(x - 4 \ne 0\) khi \(x \ne 4.\)
Do đó, điều kiện xác định của biểu thức \(A\) là \(x \ge 0\) và \(x \ne 4.\)
⦁ Xét biểu thức \(B = \frac{{4\left( {\sqrt x + 2} \right)}}{{\sqrt x - 2}}.\)
Do đó, điều kiện xác định của biểu thức \(B\) là \(x \ge 0,\,\,\sqrt x - 2 \ne 0,\) tức là \(x \ge 0\) và \(x \ne 4\).
Vậy điều kiện xác định của biểu thức \(A\) và biểu thức \(B\) đều là \(x \ge 0,\,\,x \ne 4.\)
Lời giải
b) Thay \(x = 196\,\,\left( {{\rm{TM}}} \right)\) vào biểu thức \(B\) ta được:
\[B = \frac{{4 \cdot \left( {\sqrt {196} + 2} \right)}}{{\sqrt {196} - 2}} = \frac{{4 \cdot \left( {14 + 2} \right)}}{{14 - 2}} = \frac{{4 \cdot 16}}{{12}} = \frac{{16}}{3}\].
Vậy với \(x = 196\) thì giá trị của biểu thức \[B = \frac{{16}}{3}\].
Lời giải
c) Với \(x \ge 0, x \ne 4\), ta có:
\(A = \frac{{\sqrt x + 2}}{{\sqrt x - 2}} - \frac{{\sqrt x - 2}}{{\sqrt x + 2}} + \frac{{4x}}{{x - 4}}\)
\[ = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} + \frac{{4x}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\]
\[ = \frac{{x + 4\sqrt x + 4 - x + 4\sqrt x - 4 + 4x}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\]
\[ = \frac{{4\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \frac{{4\sqrt x }}{{\sqrt x - 2}}\]
\[ = \frac{{4x + 8\sqrt x }}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\].
Vậy với \(x \ge 0, x \ne 4\) thì \[A = \frac{{4\sqrt x }}{{\sqrt x - 2}}\].
Lời giải
d) Với \(x \ge 0, x \ne 4,\) ta có
\(P = A:B\)\[ = \frac{{4\sqrt x }}{{\sqrt x - 2}}:\frac{{4\left( {\sqrt x + 2} \right)}}{{\sqrt x - 2}}\]\[ = \frac{{4\sqrt x }}{{\sqrt x - 2}} \cdot \frac{{\sqrt x - 2}}{{4\left( {\sqrt x + 2} \right)}} = \frac{{\sqrt x }}{{\sqrt x + 2}}\].
Với \(x \ge 0, x \ne 4\) thì \[\sqrt P \] luôn có nghĩa.
Xét hiệu: \[P - 1 = \frac{{\sqrt x }}{{\sqrt x + 2}} - 1 = \frac{{\sqrt x - \sqrt x - 2}}{{\sqrt x + 2}} = \frac{{ - 2}}{{\sqrt x + 2}}\].
Ta thấy: \[ - 2 < 0\]; \[\sqrt x + 2 > 0\] với \(x \ge 0, x \ne 4\).
Khi đó \[\frac{{ - 2}}{{\sqrt x + 2}} < 0\] suy ra \[P - 1 < 0\] nên \[P < 1\] hay \[\sqrt P < 1\], do đó \[\sqrt P - 1 < 0\].
Mà \[\sqrt P \ge 0\] nên \[\sqrt P \left( {\sqrt P - 1} \right) \le 0\] suy ra \[P - \sqrt P \le 0\] hay \[P \le \sqrt P \].
Vậy với \(x \ge 0\,, \,x \ne 4\) thì \[P \le \sqrt P \].
Đoạn văn 2
(3,5 điểm)
Lời giải
a) Điều kiện xác định: \(x \ne \frac{1}{3},\,\,x \ne - \frac{1}{3}.\)
Ta có: \(\frac{{1 - 3x}}{{1 + 3x}} - \frac{{1 + 3x}}{{1 - 3x}} = \frac{{12}}{{1 - 9{x^2}}}\)
\(\frac{{{{\left( {1 - 3x} \right)}^2}}}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}} - \frac{{{{\left( {1 + 3x} \right)}^2}}}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}} = \frac{{12}}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}}\)
\(\frac{{{{\left( {1 - 3x} \right)}^2} - {{\left( {1 + 3x} \right)}^2}}}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}} = \frac{{12}}{{\left( {1 + 3x} \right)\left( {1 - 3x} \right)}}\)
\({\left( {1 - 3x} \right)^2} - {\left( {1 + 3x} \right)^2} = 12\)
\(\left( {1 - 3x - 1 - 3x} \right)\left( {1 - 3x + 1 + 3x} \right) = 12\)
\( - 6x \cdot 2 = 12\)
\( - 12x = 12\)
\(x = - 1\) (thỏa mãn).
Vậy phương trình có nghiệm \(x = - 1\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
3. Mức lương tối thiểu theo quy định ở Pháp năm 2022 là \(10,25\,\,\euro \) cho mỗi giờ làm việc trong dịp hè, Laurent David làm thêm tại một khách sạn theo mức lương tối thiểu theo quy định và anh ấy muốn kiếm được ít nhất \(1\,\,500\,\,\euro \) trong mùa hè này.
a) Hãy viết một bất phương trình mô tả tình huống này.
b) Hỏi anh ấy cần làm việc ít nhất bao nhiêu giờ để kiếm được số tiền trên (€ là viết tắt của Euro, là loại tiền tệ của 20 nước thuộc liên minh Châu Âu sử dụng chung).
3. Mức lương tối thiểu theo quy định ở Pháp năm 2022 là \(10,25\,\,\euro \) cho mỗi giờ làm việc trong dịp hè, Laurent David làm thêm tại một khách sạn theo mức lương tối thiểu theo quy định và anh ấy muốn kiếm được ít nhất \(1\,\,500\,\,\euro \) trong mùa hè này.
a) Hãy viết một bất phương trình mô tả tình huống này.
b) Hỏi anh ấy cần làm việc ít nhất bao nhiêu giờ để kiếm được số tiền trên (€ là viết tắt của Euro, là loại tiền tệ của 20 nước thuộc liên minh Châu Âu sử dụng chung).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
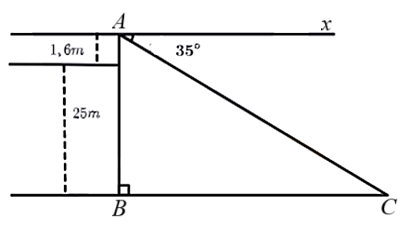
(1,5 điểm) Một người có tầm mắt cao \[1,6{\rm{ m}}\] đứng trên sân thượng của một tòa nhà cao \[{\rm{25 m}}\] nhìn thấy một chiếc xe đang đứng yên với góc nghiêng xuống \[35^\circ \] (như hình vẽ).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
(2,5 điểm) Cho nửa đường tròn \(\left( O \right)\) và đường kính \(AB\). Từ \[A\] và \[B\] kẻ hai tiếp tuyến \[Ax,\,\,By.\] Qua điểm \[M\] thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến \[Ax,\,\,By\] lần lượt ở \[C\] và \[D\]. Các đường thẳng \[AD\] và \[BC\] cắt nhau tại \[N\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.