Bộ 5 đề thi cuối kì 1 Toán 9 Kết nối tri thức (Tự luận) có đáp án - Đề 5
36 người thi tuần này 4.6 294 lượt thi 15 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 5
226 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 4
216 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 3
219 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 2
213 lượt thi
14 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 1
248 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 5
239 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 4
240 lượt thi
14 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 3
242 lượt thi
15 câu hỏi
Danh sách câu hỏi:
Đoạn văn 1
(2,0 điểm) Cho hai biểu thức: và .
Lời giải
a) ⦁ Xét biểu thức \(A = \frac{{\sqrt x + 2}}{{\sqrt x + 3}}\).
Ta có \(\sqrt x + 3 > 0\) với mọi \(x \ge 0\) nên điều kiện xác định của biểu thức \(A\) là \(x \ge 0.\)
⦁ Xét biểu thức \(B = \frac{{\sqrt x + 5}}{{\sqrt x + 1}} + \frac{{7 - \sqrt x }}{{x - 1}}\).
Ta có \(\sqrt x + 1 > 0\) với mọi \(x \ge 0\) nên điều kiện xác định của biểu thức \(B\) là \(x \ge 0,\,\,x \ne 1.\)
Lời giải
b) Thay \(x = 16\) (thỏa mãn điều kiện) vào biểu thức \(A\), ta được:
\(A = \frac{{\sqrt {16} + 2}}{{\sqrt {16} + 3}} = \frac{{4 + 2}}{{4 + 3}} = \frac{6}{7}\).
Vậy \(A = \frac{6}{7}\) khi \(x = 16\).
Lời giải
c) Với \(x \ge 0;x \ne 1\), ta có:
\(B = \frac{{\sqrt x + 5}}{{\sqrt x + 1}} + \frac{{7 - \sqrt x }}{{x - 1}} = \frac{{\left( {\sqrt x + 5} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{7 - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\)
\( = \frac{{x + 4\sqrt x - 5 + 7 - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{x + 3\sqrt x + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\)
\( = \frac{{x + \sqrt x + 2\sqrt x + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\sqrt x + 2}}{{\sqrt x - 1}}.\)
Vậy với \(x \ge 0;x \ne 1\) thì \(B = \frac{{\sqrt x + 2}}{{\sqrt x - 1}}\).
Lời giải
Hướng dẫn giải
d) Với \(x \ge 0;x \ne 1\), ta có:
Ta lại có: \(\sqrt x \ge 0\) nên \(\sqrt x + 3 \ge 3,\) suy ra \(\frac{4}{{\sqrt x + 3}} \le \frac{4}{3}\), do đó \(1 - \frac{4}{{\sqrt x + 3}} \ge - \frac{1}{3}\).
\(\sqrt x \ge 0\) nên \(\sqrt x + 3 \ge 3 > 0,\) suy ra \(\frac{4}{{\sqrt x + 3}} > 0\), do đó \(1 - \frac{4}{{\sqrt x + 3}} < 1\).
Như vậy, \( - \frac{1}{3} \le P < 1\).
Mà \(P\) nhận giá trị nguyên nên \(P = 0.\)
Với \(P = 0,\) ta có: \(1 - \frac{4}{{\sqrt x + 3}} = 0,\) suy ra \(\frac{4}{{\sqrt x + 3}} = 1,\) do đó \(\sqrt x + 3 = 4\) nên \(\sqrt x = 1,\) hay \(x = 1\) (không thỏa mãn điều kiện).
Vậy không có giá trị \(x\) để biểu thức \(P = \frac{A}{B}\) nhận giá trị nguyên.
Đoạn văn 2
(3,5 điểm)
Lời giải
a) Điều kiện xác định: \[x \ne 1;x \ne 3\].
Ta có: \[\frac{{x + 1}}{{x - 3}} - \frac{{x + 3}}{{x - 1}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[\frac{{\left( {x + 1} \right)\left( {x - 1} \right)}}{{\left( {x - 3} \right)\left( {x - 1} \right)}} - \frac{{\left( {x + 3} \right)\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[\frac{{{x^2} - 1 - \left( {{x^2} - 9} \right)}}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[{x^2} - 1 - {x^2} + 9 = 8x - 5\]
\[8 + 5 = 8x\]
\[8x = 13\]
\[x = \frac{{13}}{8}\] (thỏa mãn).
Vậy phương trình có nghiệm là \[x = \frac{{13}}{8}\].Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
3. Cho hình tam giác và hình chữ nhật có kích thước hình bên dưới. Biết chu vi của hình tam giác luôn lớn hơn chu vi của hình chữ nhật.
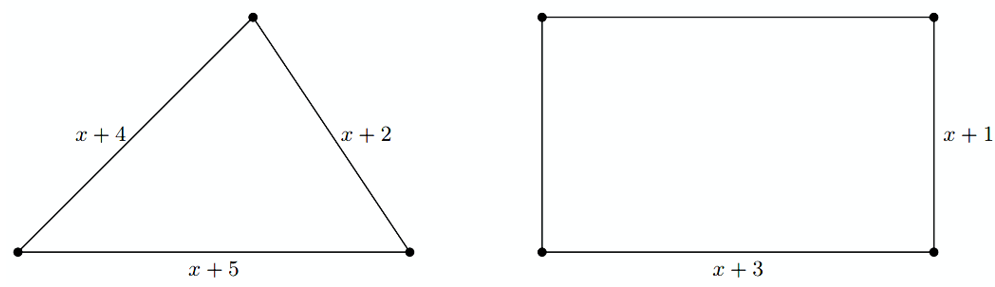
a) Hãy viết bất phương trình phù hợp với dữ liệu đề bài.
b) Tìm giá trị nguyên lớn nhất có thể của \(x\) thỏa mãn yêu cầu bài toán.
3. Cho hình tam giác và hình chữ nhật có kích thước hình bên dưới. Biết chu vi của hình tam giác luôn lớn hơn chu vi của hình chữ nhật.
a) Hãy viết bất phương trình phù hợp với dữ liệu đề bài.
b) Tìm giá trị nguyên lớn nhất có thể của \(x\) thỏa mãn yêu cầu bài toán.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
(1,5 điểm) Hai người A và B đứng cùng bờ sông nhìn ra một cồn C nổi giữa sông. Người A nhìn ra cồn với một góc \(43^\circ \) so với bờ sông, người B nhìn ra cồn với một góc \(28^\circ \) so với bờ sông. Khoảng cách của cồn và bờ sông hai người đứng chính là độ dài đoạn thẳng \(CH.\) Hai người đứng cách nhau \(250{\rm{ m}}{\rm{.}}\)
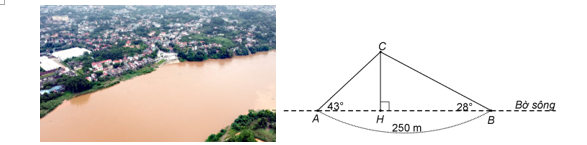
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
(2,5 điểm) Cho đường tròn \(\left( {O;R} \right)\), đường kính \(AB = 2R\). Vẽ hai tiếp tuyến \(d,\,\,d'\) của đường tròn \(\left( {O;R} \right)\) lần lượt tại \(A,\,\,B\). Trên đường thẳng \(d\) lấy điểm \(C\), từ \(O\) kẻ đường thẳng vuông góc với \(OC\) cắt đường thẳng \(d'\) ở \(D\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập