(3,5 điểm)
1. Giải các phương trình, bất phương trình sau:
a) \[\frac{{x + 1}}{{x - 3}} - \frac{{x + 3}}{{x - 1}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\].
(3,5 điểm)
1. Giải các phương trình, bất phương trình sau:
a) \[\frac{{x + 1}}{{x - 3}} - \frac{{x + 3}}{{x - 1}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\].Quảng cáo
Trả lời:
a) Điều kiện xác định: \[x \ne 1;x \ne 3\].
Ta có: \[\frac{{x + 1}}{{x - 3}} - \frac{{x + 3}}{{x - 1}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[\frac{{\left( {x + 1} \right)\left( {x - 1} \right)}}{{\left( {x - 3} \right)\left( {x - 1} \right)}} - \frac{{\left( {x + 3} \right)\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[\frac{{{x^2} - 1 - \left( {{x^2} - 9} \right)}}{{\left( {x - 3} \right)\left( {x - 1} \right)}} = \frac{{8x - 5}}{{\left( {x - 3} \right)\left( {x - 1} \right)}}\]
\[{x^2} - 1 - {x^2} + 9 = 8x - 5\]
\[8 + 5 = 8x\]
\[8x = 13\]
\[x = \frac{{13}}{8}\] (thỏa mãn).
Vậy phương trình có nghiệm là \[x = \frac{{13}}{8}\].Câu hỏi cùng đoạn
Câu 2:
Giải các phương trình, bất phương trình sau:
b) \[\frac{{4x + 9}}{3} + \frac{1}{2} \ge \frac{{2x - 1}}{4}\].
Giải các phương trình, bất phương trình sau:
b) \[\frac{{4x + 9}}{3} + \frac{1}{2} \ge \frac{{2x - 1}}{4}\]
\[\frac{{4\left( {4x + 9} \right)}}{{12}} + \frac{6}{{12}} \ge \frac{{3\left( {2x - 1} \right)}}{{12}}\]
\[4\left( {4x + 9} \right) + 6 \ge 3\left( {2x - 1} \right)\]
\[16x + 36 + 6 \ge 6x - 3\]
\[16x + 42 \ge 6x - 3\]
\[16x - 6x \ge - 3 - 42\]
\[10x \ge - 45\]
\[x \ge - \frac{9}{2}.\]
Vậy bất phương trình có nghiệm là \[x \ge - \frac{9}{2}.\]
Câu 3:
Giải các phương trình, bất phương trình sau:
c) \(\sqrt {4x + 20} = 20\).
c) \(\sqrt {4x + 20} = 20\) (ĐKXĐ: \(x \ge - 5)\)
\(\sqrt {4\left( {x + 5} \right)} = 20\)
\(2\sqrt {x + 5} = 20\)
\(\sqrt {x + 5} = 10\)
\(x + 5 = 100\)
\(x = 95\) (thỏa mãn).
Vậy phương trình đã cho là \(x = 95\).
Câu 4:
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một trường tổ chức cho 235 học sinh và 15 giáo viên đi trải nghiệm trồng nông sản ở khu nông nghiệp công nghệ cao. Nhân dịp Lễ Giáng Sinh nên giá vé trải nghiệm được giảm 5% cho mỗi vé của giáo viên và 8% cho mỗi vé của học sinh, vì vậy nhà trường chỉ phải trả số tiền là 44 498 000 đồng. Hỏi giá vé của mỗi giáo viên và mỗi học sinh khi chưa giảm là bao nhiêu nghìn đồng, biết rằng tổng chi phí cho vé trải nghiệm khi chưa giảm là 48 250 000 đồng?
2. Giải bài toán sau bằng cách lập hệ phương trình:
Một trường tổ chức cho 235 học sinh và 15 giáo viên đi trải nghiệm trồng nông sản ở khu nông nghiệp công nghệ cao. Nhân dịp Lễ Giáng Sinh nên giá vé trải nghiệm được giảm 5% cho mỗi vé của giáo viên và 8% cho mỗi vé của học sinh, vì vậy nhà trường chỉ phải trả số tiền là 44 498 000 đồng. Hỏi giá vé của mỗi giáo viên và mỗi học sinh khi chưa giảm là bao nhiêu nghìn đồng, biết rằng tổng chi phí cho vé trải nghiệm khi chưa giảm là 48 250 000 đồng?
2. Gọi \[x,{\rm{ }}y\] (nghìn đồng) lần lượt là giá vé của mỗi giáo viên và mỗi học sinh khi chưa giảm giá \(\left( {x,y > 0} \right).\)
Tổng chi phí cho vé trải nghiệm khi chưa giảm là 48 250 000 đồng nên ta có
\(15x + 235y = 48\,\,250\) hay \(3x + 47y = 9\,\,650\) (1)
Nhân dịp Lễ Giáng Sinh nên giá vé trải nghiệm được giảm 5% cho mỗi vé của giáo viên và 8% cho mỗi vé của học sinh nên ta có
\(15 \cdot 95\% x + 235 \cdot 92\% y = 44\,\,498\) hay \(14,25x + 216,2y = 44\,\,498\) (2)
Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}3x + 47y = 9\,\,650\\14,25x + 216,2y = 44\,\,498\end{array} \right.\)
Giải hệ phương trình ta được \(\left\{ \begin{array}{l}x = 240\\y = 190\end{array} \right.\) (thoả điều kiện)
Vậy giá vé của mỗi giáo viên và mỗi học sinh khi chưa giảm giá lần lượt là 240 nghìn đồng và 190 nghìn đồng.
Câu 5:
3. Cho hình tam giác và hình chữ nhật có kích thước hình bên dưới. Biết chu vi của hình tam giác luôn lớn hơn chu vi của hình chữ nhật.
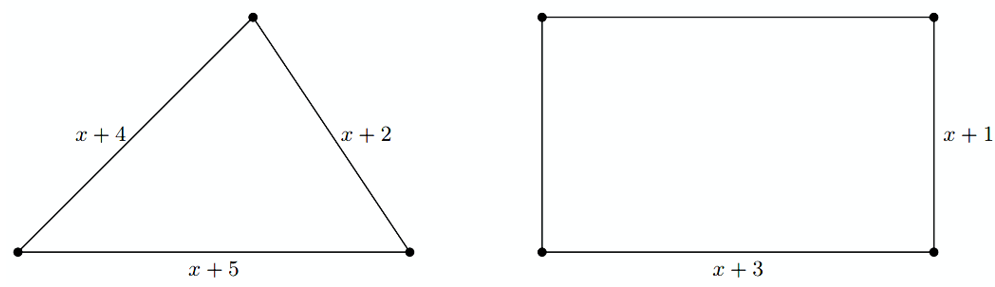
a) Hãy viết bất phương trình phù hợp với dữ liệu đề bài.
b) Tìm giá trị nguyên lớn nhất có thể của \(x\) thỏa mãn yêu cầu bài toán.
3. Cho hình tam giác và hình chữ nhật có kích thước hình bên dưới. Biết chu vi của hình tam giác luôn lớn hơn chu vi của hình chữ nhật.

a) Hãy viết bất phương trình phù hợp với dữ liệu đề bài.
b) Tìm giá trị nguyên lớn nhất có thể của \(x\) thỏa mãn yêu cầu bài toán.
3. a) Hình tam giác có kích thước ba cạnh lần lượt là \(x + 2\,;\,\,x + 4\,;\,\,x + 5\) (đvđd).
Khi đó, chu vi hình tam giác là \(x + 2 + x + 4 + x + 5 = 3x + 11\) (đvđd).
Hình chữ nhật có chiều dài \(x + 3\) (đvđd) và chiều rộng \(x + 1\) (đvđd).
Khi đó, chu vi hình chữ nhật là \[2\left( {x + 3 + x + 1} \right) = 4x + 8\] (đvđd).
Vì chu vi của hình tam giác luôn lớn hơn chu vi của hình chữ nhật nên ta có \(3x + 11 > 4x + 8\).
Vậy bất phương trình cần tìm là: \(3x + 11 > 4x + 8\).
b) Giải bất phương trình:
\(3x + 11 > 4x + 8\)
\(4x - 3x < 11 - 8\)
\(x < 3.\)
Mà \(x\) là giá trị nguyên lớn nhất có thể nên \(x = 2.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
– Gọi \(x\) là số lần giảm giá \(10\,\,000\) đồng \(\left( {x \in \mathbb{N},\,\,0 \le x < 20} \right).\)
Giá bán mỗi sản phẩm sau khi giảm giá là: \(200 - 10x\) (nghìn đồng).
Số lượng sản phẩm bán ra sau khi giảm giá là: \(100 + 20x\) (chiếc).
Doanh thu \(T\left( x \right)\) của cửa hàng được tính bằng cách nhân giá bán mỗi sản phẩm với số lượng sản phẩm bán ra:
\(T\left( x \right) = \left( {200 - 10x} \right)\left( {100 + 20x} \right)\)
\( = 200.\left( {100 + 20x} \right) - 10x\left( {100 + 20x} \right)\)
\( = 20\,\,000 + 4\,\,000x - 1\,\,000x - 200{x^2}\)
\( = 20\,\,000 + 3\,\,000x - 200{x^2}\)
\( = - 200\left( {{x^2} - 15x + 7,{5^2}} \right) + 31\,\,250\)
\( = - 200{\left( {x - 7,5} \right)^2} + 31\,\,250\) (nghìn đồng).
Nhận thấy \( - 200{\left( {x - 7,5} \right)^2} + 31\,\,250 \le 31\,\,250\).
Dấu “=” xảy ra khi và chỉ khi \(x - 7,5 = 0\) khi \(x = 7,5\).
Do \(x\) phải là số nguyên dương nên \(x = 7,5\) không thỏa mãn.
– Ta thấy rằng \(T\left( x \right) = - 200{\left( {x - 7,5} \right)^2} + 31\,\,250\) lớn nhất khi \({\left( {x - 7,5} \right)^2}\) nhỏ nhất.
Do giá trị của \(T\left( x \right)\) phụ thuộc \(x - 7,5\) và \(x\) nguyên nên ta xét các trường hợp sau:
⦁ Với \(x - 7,5 > 0\) hay \(x > 7,5\)
Mà \(x\) nguyên dương và \({\left( {x - 7,5} \right)^2}\) nhỏ nhất, nên ta lấy giá trị \(x = 8.\)
Khi đó, \(T\left( 8 \right) = 31\,\,200\) (nghìn đồng).
⦁ Với \(x - 7,5 < 0\) hay \(x < 7,5\)
Mà \(x\) nguyên dương và \({\left( {x - 7,5} \right)^2}\) nhỏ nhất, nên ta lấy giá trị \(x = 7.\)
Khi đó, \(T\left( 7 \right) = 31\,\,200\) (nghìn đồng).
Nhận thấy cả hai giá trị \(x = 7,\,\,x = 8\) đều cho doanh thu \(T = 31\,\,200\) (nghìn đồng) hay \(T = 31\,\,200\,\,000\) đồng. Do đó, cửa hàng nên giảm giá \(70\,\,000\) đồng hoặc \(80\,\,000\) đồng để thu được doanh thu cao nhất.
Lời giải
a) ⦁ Xét biểu thức \(A = \frac{{\sqrt x + 2}}{{\sqrt x + 3}}\).
Ta có \(\sqrt x + 3 > 0\) với mọi \(x \ge 0\) nên điều kiện xác định của biểu thức \(A\) là \(x \ge 0.\)
⦁ Xét biểu thức \(B = \frac{{\sqrt x + 5}}{{\sqrt x + 1}} + \frac{{7 - \sqrt x }}{{x - 1}}\).
Ta có \(\sqrt x + 1 > 0\) với mọi \(x \ge 0\) nên điều kiện xác định của biểu thức \(B\) là \(x \ge 0,\,\,x \ne 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.