Bộ 5 đề thi cuối kì 1 Toán 9 Kết nối tri thức (Tự luận) có đáp án - Đề 2
43 người thi tuần này 4.6 294 lượt thi 15 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 5
226 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 4
216 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 3
219 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 2
213 lượt thi
14 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Chân trời sáng tạo (Tự luận) có đáp án - Đề 1
248 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 5
239 lượt thi
15 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 4
240 lượt thi
14 câu hỏi
Bộ 5 đề thi cuối kì 1 Toán 9 Cánh diều (Tự luận) có đáp án - Đề 3
242 lượt thi
15 câu hỏi
Danh sách câu hỏi:
Đoạn văn 1
(2,0 điểm) Cho hai biểu thức: và với
Lời giải
a) ⦁ Xét biểu thức \(A = \frac{{x + 3}}{{\sqrt x - 2}}\).
Điều kiện xác định của biểu thức \(A\) và \(x \ge 0\) và \(\sqrt x - 2 \ne 0\) hay \(x \ge 0,\,\,x \ne 4.\)
⦁ Xét biểu thức \(B = \frac{{\sqrt x - 1}}{{\sqrt x + 2}} + \frac{{5\sqrt x - 2}}{{x - 4}}\).
Điều kiện xác định của biểu thức \(B\) là \(x \ge 0,\,\,\sqrt x + 2 \ne 0\) và \(x - 4 \ne 0.\)
Với \(x \ge 0\) ta thấy \(\sqrt x + 2 > 0\) và \(x - 4 \ne 0\) khi \(x \ne 4.\)
Vậy, điều kiện xác định của biểu thức \(A\) và biểu thức \(B\) đều là \(x \ge 0,\,\,x \ne 4.\)
Lời giải
b) Với \(x = 16\) (thỏa mãn điều kiện), ta có
\(A = \frac{{16 + 3}}{{\sqrt {16} - 2}} = \frac{{19}}{{4 - 2}} = \frac{{19}}{2}\).
Vậy khi \(x = 16\) thì giá trị của biểu thức \(A\) bằng \(\frac{{19}}{2}\).
Lời giải
c) Với \(x > 0,\,\,x \ne 4\), ta có
\( = \frac{{x - 3\sqrt x + 2 + 5\sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} = \frac{{x + 2\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}\)
\( = \frac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} = \frac{{\sqrt x }}{{\sqrt x - 2}}\).
Lời giải
Hướng dẫn giải
d) Ta có \(P = \frac{A}{B} = \frac{{x + 3}}{{\sqrt x - 2}}:\frac{{\sqrt x }}{{\sqrt x - 2}} = \frac{{x + 3}}{{\sqrt x }}\).
Do đó \(P \le 4\) khi \(\frac{{x + 3}}{{\sqrt x }} \le 4\) suy ra \(\frac{{x + 3}}{{\sqrt x }} - 4 \le 0\) hay \(\frac{{x + 3 - 4\sqrt x }}{{\sqrt x }} \le 0\).
Do \(\sqrt x > 0\) nên để \(\frac{{x + 3 - 4\sqrt x }}{{\sqrt x }} \le 0\) thì \(x + 3 - 4\sqrt x \le 0\).
Ta có \(x + 3 - 4\sqrt x = x - 4\sqrt x + 4 - 1 = {\left( {\sqrt x - 2} \right)^2} - 1\).
Do đó \(x + 3 - 4\sqrt x \le 0\) khi \({\left( {\sqrt x - 2} \right)^2} - 1 \le 0\) suy ra \[ - 1 \le \;\sqrt x - 2 \le 1\] hay \[1 \le \;\sqrt x \le 3\] từ dó suy ra \[1 \le \;x \le 9\].
Vì \[x\] nguyên nên ta có \[x \in \left\{ {1\,;\,\,2\,;\,\,3\,;\,\,4\,;\,\,5\,;\,\,6\,;\,\,7\,;\,\,8\,;\,\,9} \right\}.\]
Đoạn văn 2
(3,5 điểm)
Lời giải
a) Điều kiện xác định: \(x \ne 1,\,\,x \ne 0.\)
Ta có: \(\frac{4}{{x - 1}} - \frac{3}{x} = \frac{{4x}}{{x\left( {x - 1} \right)}}\)
\(\frac{{4x}}{{x\left( {x - 1} \right)}} - \frac{{3\left( {x - 1} \right)}}{{x\left( {x - 1} \right)}} = \frac{{4x}}{{x\left( {x - 1} \right)}}\)
\(\frac{{4x - 3\left( {x - 1} \right)}}{{x\left( {x - 1} \right)}} = \frac{{4x}}{{x\left( {x - 1} \right)}}\)
\(4x - 3x + 3 = 4x\)
\(4x - 3x - 4x = - 3\)
\( - 3x = - 3\)
\(x = 1\) (không thỏa mãn điều kiện).
Vậy phương trình đã cho vô nghiệm.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
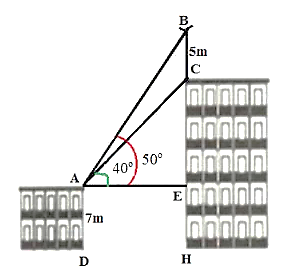
(1,5 điểm) Trên nóc của một tòa nhà có một cột ăng – ten cao \(5{\rm{ m}}\). Từ vị trí quan sát \(A\) cao \(7{\rm{ m}}\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và đỉnh \(C\) của một cột ăng – ten dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
(2,5 điểm) Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) sao cho \(OM = \frac{8}{5}R.\) Từ \(M\) vẽ hai tiếp tuyến \(MA\) và \(MB\) của đường tròn \(\left( O \right)\) (với \(A,B\) là hai tiếp điểm), đường thẳng \(AB\) cắt \(OM\) tại \(K\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập