(1,5 điểm) Trên nóc của một tòa nhà có một cột ăng – ten cao \(5{\rm{ m}}\). Từ vị trí quan sát \(A\) cao \(7{\rm{ m}}\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và đỉnh \(C\) của một cột ăng – ten dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang.
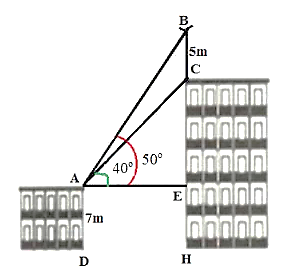
a) Viết tỉ số lượng giác sin và tan của góc \(ABE\) theo \(AB,\,\,BE,\,\,AE.\)
(1,5 điểm) Trên nóc của một tòa nhà có một cột ăng – ten cao \(5{\rm{ m}}\). Từ vị trí quan sát \(A\) cao \(7{\rm{ m}}\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và đỉnh \(C\) của một cột ăng – ten dưới góc \(50^\circ \) và \(40^\circ \) so với phương nằm ngang.
a) Viết tỉ số lượng giác sin và tan của góc \(ABE\) theo \(AB,\,\,BE,\,\,AE.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Xét tam giác \(ABE\) vuông tại \(E\), ta có: \(\sin \widehat {ABE} = \frac{{AE}}{{AB}},\,\,\tan \widehat {ABE} = \frac{{AE}}{{BE}}.\)
Câu hỏi cùng đoạn
Câu 2:
b) Tính chiều cao của tòa nhà.
Giải bởi Vietjack
b) Chiều cao của tòa nhà chính là độ dài đoạn thẳng \(BH\).
Xét tam giác \(CAE\) vuông tại \(E\), ta có:
\(CE = AE.\tan \widehat {CAE} = AE.\tan 40^\circ {\rm{ }}\left( {\rm{m}} \right)\) (1).
Xét tam giác \(BAE\) vuông ở \(E\), ta có:
\(BE = AE.\tan \widehat {BAE} = AE.\tan 50^\circ {\rm{ }}\left( {\rm{m}} \right)\) (2).
Từ (1) và (2) suy ra \(BC = BE - CE = AE\tan 50^\circ - AE\tan 40^\circ \)
\(BC = AE\left( {\tan 50^\circ - \tan 40^\circ } \right)\)
\(5 = AE\left( {\tan 50^\circ - \tan 40^\circ } \right)\)
\(AE = \frac{5}{{\tan 50^\circ - \tan 40^\circ }}{\rm{ }}\left( {\rm{m}} \right)\).
Suy ra \(CE = AE \cdot \tan \widehat {CAE} = \frac{5}{{\tan 50^\circ - \tan 40^\circ }} \cdot \tan 40^\circ \approx 11,9{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)
Chiều cao của tòa nhà là: \(5 + 11,9 + 7 \approx 23,9{\rm{ }}\left( {\rm{m}} \right)\).
Vậy tòa nhà cao \(23,9{\rm{ m}}.\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Với a là chiều dài của hai ngăn bể cá. Ta có \(V = abc = 750\) (1)
Diện tích các miếng hình là : \(S = ab + 2ac + 2bc\).
Ta có \(\frac{S}{{abc}} = \frac{1}{c} + \frac{2}{b} + \frac{3}{a}\).
Áp dụng bất đẳng thức Cauchy cho 3 số \(\frac{1}{c};\,\,\frac{2}{b};\,\,\frac{3}{a}\) ta được
\(\frac{S}{{abc}} = \frac{1}{c} + \frac{2}{b} + \frac{3}{a} \ge 3\sqrt[3]{{\frac{1}{c} \cdot \frac{2}{b} \cdot \frac{3}{a}}} = \frac{{3\sqrt[3]{6}}}{{\sqrt {abc} }} = \frac{{3\sqrt[3]{6}}}{{\sqrt {750} }}.\)
Dấu xảy ra khi \(\left\{ \begin{array}{l}\frac{1}{c} = \frac{2}{b} = \frac{3}{a}\\abc = 750\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}2a = 3b\\a = 3c\\b = 2c\\abc = 750\end{array} \right.\).
Khi đó, ta có \(3c \cdot 2c \cdot c = 750\) hay \(6{c^3} = 750\) nên \({c^3} = 125\) suy ra \(c = 5\).
Do đó \(a = 3c = 15\,;\,\,b = 2c = 10\,;\,\,c = 5.\)
Vậy các kích thước\(a = 15\,;\,\,b = 10\,;\,\,c = 5\) để lượng inox cần sử dụng là ít nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Điều kiện xác định: \(x \ne 1,\,\,x \ne 0.\)
Ta có: \(\frac{4}{{x - 1}} - \frac{3}{x} = \frac{{4x}}{{x\left( {x - 1} \right)}}\)
\(\frac{{4x}}{{x\left( {x - 1} \right)}} - \frac{{3\left( {x - 1} \right)}}{{x\left( {x - 1} \right)}} = \frac{{4x}}{{x\left( {x - 1} \right)}}\)
\(\frac{{4x - 3\left( {x - 1} \right)}}{{x\left( {x - 1} \right)}} = \frac{{4x}}{{x\left( {x - 1} \right)}}\)
\(4x - 3x + 3 = 4x\)
\(4x - 3x - 4x = - 3\)
\( - 3x = - 3\)
\(x = 1\) (không thỏa mãn điều kiện).
Vậy phương trình đã cho vô nghiệm.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập