(2,5 điểm) Cho đường tròn \[\left( {O;R} \right)\] và một điểm \[A\] nằm ngoài đường tròn \[\left( O \right)\]. Từ \[A\] vẽ hai tiếp tuyến \[AB,AC\] của đường tròn \[\left( O \right)\] (\[B,\,\,C\] là hai tiếp điểm). Gọi \[H\] là giao điểm của \[OA\] và \[BC.\] Tia \[AO\] cắt đường tròn \[\left( O \right)\] tại \[M,N\] (\[M\] nằm giữa \[A\] và \[N\]).
a) Chứng minh \[OA \bot BC\] và \[AM \cdot AN = AH \cdot AO = A{O^2} - {R^2}.\]
(2,5 điểm) Cho đường tròn \[\left( {O;R} \right)\] và một điểm \[A\] nằm ngoài đường tròn \[\left( O \right)\]. Từ \[A\] vẽ hai tiếp tuyến \[AB,AC\] của đường tròn \[\left( O \right)\] (\[B,\,\,C\] là hai tiếp điểm). Gọi \[H\] là giao điểm của \[OA\] và \[BC.\] Tia \[AO\] cắt đường tròn \[\left( O \right)\] tại \[M,N\] (\[M\] nằm giữa \[A\] và \[N\]).
a) Chứng minh \[OA \bot BC\] và \[AM \cdot AN = AH \cdot AO = A{O^2} - {R^2}.\]
Quảng cáo
Trả lời:
![a) Chứng minh \[OA \bot BC\] và \[AM \cdot AN = AH \cdot AO = A{O^2} - {R^2}.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/2-1766496288.png)
a) ⦁ Xét đường tròn \[\left( O \right)\] có \[AB,AC\] là hai tiếp cắt nhau tại \[A\] nên \[AB = AC\](tính chất hai tiếp tuyến cắt nhau). Do đó \[A\] thuộc đường trung trực \[BC\].
Mặt khác, \[OB = OC = R\] nên \[O\] thuộc trung trực của đoạn thẳng \[BC\].
Suy ra \(OA\) là đường trung trực của đoạn thẳng \(BC\), do đó \[OA \bot BC\] tại \[H\].
⦁ Vì \(AB\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B\) nên \(AB \bot OB\) tại \(B.\)
Xét \[\Delta HAB\] và \[\Delta BAO\] có: \(\widehat {AHB} = \widehat {ABO} = 90^\circ \) và \(\widehat {OAB}\) là góc chung.
Do đó (g.g)
Suy ra \[\frac{{HA}}{{BA}} = \frac{{AB}}{{AO}}\] hay \[AH \cdot AO = A{B^2}\] (1).
Xét \(\Delta OAB\) vuông tại \(B,\) ta có: \[A{B^2} = A{O^2} - O{B^2} = A{O^2} - {R^2}\] (định lí Pythagore). (2)
Lại có:
\[AM \cdot AN = \left( {AO - OM} \right)\left( {AO + ON} \right)\]
\[ = A{O^2} + AO \cdot ON - OM \cdot AO - OM \cdot ON\]
\[ = A{O^2} - OM \cdot ON\]\[ = A{O^2} - {R^2}\] (vì \(OM = ON = R)\) (3)
Từ (1), (2), (3) suy ra \[AM \cdot AN = AH \cdot AO = A{O^2} - {R^2}.\]
Câu hỏi cùng đoạn
Câu 2:
b) Kẻ đường kính \[BD\], gọi \[E\] là hình chiếu của \[C\] trên \[BD\], \[K\] là giao điểm của \[AD\] và \[CE\]. Chứng minh rằng \[K\] là trung điểm của \[CE.\]
b) Kẻ đường kính \[BD\], gọi \[E\] là hình chiếu của \[C\] trên \[BD\], \[K\] là giao điểm của \[AD\] và \[CE\]. Chứng minh rằng \[K\] là trung điểm của \[CE.\]
b) ⦁ Ta có: \[CE\,{\rm{//}}\,AB\] (cùng vuông góc với \[BD\])
Suy ra \[\frac{{EK}}{{AB}} = \frac{{DE}}{{DB}}\] (hệ quả định lí Thalès).
Do đó \[EK.BD = DE.AB\](∗).
⦁ Xét \(\Delta BCD\) có \(CO\) là đường trung tuyến ứng với cạnh \(BD\) và \(CO = BO = DO = R = \frac{{BD}}{2}\) (do \(BD\) là đường kính) nên \(\Delta BCD\) vuông tại \(C.\)
Ta có \(BC \bot CD,\,\,BC \bot OA\) nên \(CD\,{\rm{//}}\,OA\), do đó \(\widehat {AOB} = \widehat {CDE}\) (đồng vị)
Xét \[\Delta ABO\] và \[\Delta CED\] có: \(\widehat {ABO} = \widehat {CED} = 90^\circ \) và \(\widehat {AOB} = \widehat {CDE}\)
Do đó (g.g).
Suy ra \[\frac{{AB}}{{CE}} = \frac{{BO}}{{ED}}\] hay \[CE.BO = DE.AB\](∗∗).
Từ (∗) và (∗∗) suy ra \[EK.BD = CE.BO\].
Mà \[BD = 2BO\], suy ra \[EK \cdot 2BO = CE.BO\], suy ra \[2EK = CE\].
Do đó \[K\] là trung điểm của \[CE.\]
Câu 3:
c) Giả sử \[OA = 2R\], tính diện tích hình quạt giới hạn bởi bán kính \[OB,OC\] và cung lớn \[BC.\]
c) Giả sử \[OA = 2R\], tính diện tích hình quạt giới hạn bởi bán kính \[OB,OC\] và cung lớn \[BC.\]
c) Xét \(\Delta AOB\) vuông tại \(B,\) có: \(\cos \widehat {AOB} = \frac{{OB}}{{OA}} = \frac{R}{{2R}} = \frac{1}{2},\) suy ra \(\widehat {AOB} = 60^\circ .\)
Do \[AB,AC\] lần lượt là tiếp tuyến tại \[B,C\] của đường tròn \(\left( O \right)\) nên \[OA\] là tia phân giác của \(\widehat {BOC}\) (tính chất 2 tiếp tuyến cắt nhau).
Suy ra \(\widehat {BOC} = 2\widehat {AOB} = 2 \cdot 60^\circ = 120^\circ .\)
Do đó, số đo cung nhỏ \(BC\) bằng \(120^\circ \).
Suy ra, số đo cung lớn \(BC\) là \(360^\circ - 120^\circ = 240^\circ .\)
Diện tích hình quạt giới hạn bởi các bán kính \[OB,OC\] và cung lớn \[BC\] là
\(S = \frac{{\pi {R^2} \cdot 240}}{{360}} = \frac{{2\pi {R^2}}}{3}\) (đơn vị diện tích).
Vậy diện tích hình quạt giới hạn bởi các bán kính \[OB,\,\,OC\] và cung lớn \[BC\] là \(\frac{{2\pi {R^2}}}{3}\) (đvdt).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Điều kiện xác định: \(x \ne 1\) và \(x \ne - 1\).
Ta có: \(\frac{{x - 1}}{{x + 1}} - \frac{{x + 1}}{{x - 1}} = \frac{8}{{{x^2} - 1}}\)
\(\frac{{{{\left( {x - 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} - \frac{{{{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{8}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\(\frac{{{{\left( {x - 1} \right)}^2} - {{\left( {x + 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{8}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
\({\left( {x - 1} \right)^2} - {\left( {x + 1} \right)^2} = 8\)
\(\left( {x - 1 + x + 1} \right)\left( {x - 1 - x - 1} \right) = 8\)
\(2x.\left( { - 2} \right) = 8\)
\( - 4x = 8\)
\(x = - 2\) (thỏa mãn).
Vậy nghiệm của phương trình là \(x = - 2\).Lời giải
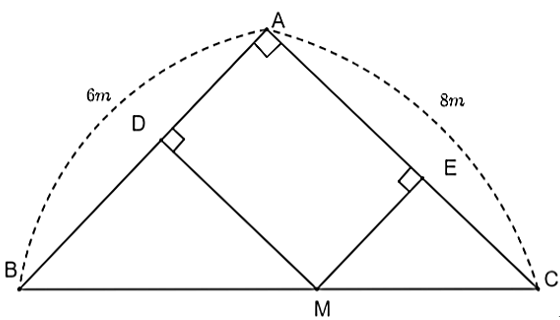
Đặt \[AD = x\,\,\left( {x > 0} \right)\].
Ta có tứ giác \[ADME\] có \[\widehat {ADE} = \widehat {DAE} = \widehat {AED} = 90^\circ \] nên \[ADME\] là hình chữ nhật. Do đó, \[AD = EM = x.\]
Chứng minh được (g.g), từ đó ta có:
\[\frac{{EM}}{{AB}} = \frac{{CE}}{{CA}}\] hay \[\frac{x}{6} = \frac{{CE}}{8}\] suy ra \[CE = \frac{4}{3}x\].
Ta có \[AE = AC - EC = 8 - \frac{4}{3}x\].
Diện tích hình chữ nhật \[ADME\] là:
\[{S_{ADME}} = AD.AE = x\left( {8 - \frac{4}{3}x} \right)\].
Ta có: \[x\left( {8 - \frac{4}{3}x} \right) = - \frac{4}{3}{x^2} + 8x = - \frac{4}{3}\left( {{x^2} - 6x} \right)\]
\[ = - \frac{4}{3}\left( {{x^2} - 6x + 9} \right) + 12\]
\[ = - \frac{4}{3}{\left( {x - 3} \right)^2} + 12\].
Vì \[{\left( {x - 3} \right)^2} \ge 0\] với mọi \(x \in \mathbb{R}\) nên \[ - \frac{4}{3}{\left( {x - 3} \right)^2} \le 0\] với mọi \(x \in \mathbb{R}\).
Do đó \[ - \frac{4}{3}{\left( {x - 3} \right)^2} + 12 \le 12\] với mọi \(x \in \mathbb{R}\).
Dấu “=” xảy ra khi \[x - 3 = 0\] khi \[x = 3.\]
Khi đó \[D\] là trung điểm của \[AB\].
Suy ra \[M\] là trung điểm của \[BC\].
Vậy diện tích lớn nhất của \[ADME\] bằng \[{\rm{12 }}{{\rm{m}}^{\rm{2}}}\] khi \[M\] là trung điểm của \[BC\].
Diện tích ao cá lớn nhất mà người đó có thể đào là \[{\rm{12 }}{{\rm{m}}^{\rm{2}}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.