Lúc 7 giờ 30 phút hai xe ô tô cùng xuất phát từ A đến B với vận tốc của mỗi xe không thay đổi trên cả quãng đường. Xe thứ hai đến B sớm hơn xe thứ nhất đúng 1 giờ. Lúc quay trở về, xe thứ nhất tăng vận tốc thêm 5 km / h, xe thứ hai vẫn giữ nguyên vận tốc như lúc đi nhưng dùng ở trạm nghỉ 36 phút, do đó xe thứ hai về đến A cùng lúc với xe thứ nhất. Biết rằng quãng đường từ A đến B là 180 km . Hỏi lúc đi, xe thứ nhất đến B lúc mấy giờ?
Lúc 7 giờ 30 phút hai xe ô tô cùng xuất phát từ A đến B với vận tốc của mỗi xe không thay đổi trên cả quãng đường. Xe thứ hai đến B sớm hơn xe thứ nhất đúng 1 giờ. Lúc quay trở về, xe thứ nhất tăng vận tốc thêm 5 km / h, xe thứ hai vẫn giữ nguyên vận tốc như lúc đi nhưng dùng ở trạm nghỉ 36 phút, do đó xe thứ hai về đến A cùng lúc với xe thứ nhất. Biết rằng quãng đường từ A đến B là 180 km . Hỏi lúc đi, xe thứ nhất đến B lúc mấy giờ?
Quảng cáo
Trả lời:
Nếu lúc quay trở về mà hai xe cùng xuất phát một lúc thì ta có lời giải bên dưới
Gọi vận tốc của xe 1 là x (km/h), x > 0
Gọi vận tốc của xe 2 là y (km/h), y > 0
Khi đi hai xe cùng xuất phát và xe hai đến B sớm hơn xe một 1 giờ, ta có phương trình:
\[\frac{{180}}{x} = \frac{{180}}{y} + 1\] (1)
Khi trở về xe một tang tốc thêm 5km/h, xe hai giữ nguyên vận tốc và dừng ở trạm nghỉ 36 phút và hai xe về đến A cùng lúc ta có phương trình: \[\frac{{180}}{{x + 5}} = \frac{{180}}{y} + \frac{{36}}{{60}}\] (2)
Giải hệ phương trình (1) và (2) ta được
Thời gian xe thứ nhất đi đến B là 4 giờ.
Vậy lúc đi xe thứ nhất đến B lúc 11 giờ 30 phút.
Nếu lúc quay trở về mà hai xe không cùng xuất phát một lúc thi ta có lời giải như sau.
Gọi vận tốc của xe 1 là x (km/h), x>0
Gọi vận tốc của xe 2 là y (km/h), y>0
Thời gian xe thứ nhất đi từ A đến B là \[\frac{{180}}{x}\](h)
Thời gian xe thứ hai đi từ A đến B là \[\frac{{180}}{y}\](h)
Thời gian xe thứ nhất đi từ B đến về A là \[\frac{{180}}{{x + 5}}\](h)
Thời gian xe thứ hai đi từ B về A ( tính cả thời gian nghỉ) là \[\frac{{180}}{y} + \frac{{36}}{{60}}\](h)
Vì lúc đi hai xe xuất phát cùng lúc và xe thứ hai đến B sớm hơn xe thứ nhất 1 giờ nên ta có phương trình \[\frac{{180}}{x} = \frac{{180}}{y} + 1\] (1)
Vì hai xe xuất phát cùng một thời điểm và về A cùng lúc nên tổng thời gian lúc đi và về của hai xe là bằng nhau nên ta có phương trình \[\frac{{180}}{x} + \frac{{180}}{{x + 5}} = \frac{{180}}{y} + \frac{{180}}{y} + \frac{{36}}{{60}} \Leftrightarrow \frac{{180}}{x} + \frac{{180}}{{x + 5}} = 2.\frac{{180}}{y} + \frac{3}{5}\](2)
Thay (1) vào (2) ta có \[\frac{{180}}{x} + \frac{{180}}{{x + 5}} = 2.\frac{{180}}{x} - 2 + \frac{3}{5} \Leftrightarrow \frac{{180}}{x} - \frac{{180}}{{x + 5}} = \frac{7}{5} \Leftrightarrow \frac{{900}}{{x\left( {x + 5} \right)}} = \frac{7}{5} \Leftrightarrow 7{x^2} + 35x - 4500 = 0(*)\]
Ta có \[\sqrt \Delta = \sqrt {127225} \]
Phương trình (*) có 2 nghiệm x=\[\frac{{ - 35 + \sqrt {127225} }}{{14}}\]( thỏa mãn)
X=\[\frac{{ - 35 - \sqrt {127225} }}{{14}}\]( không thỏa mãn)
Với x=\[\frac{{ - 35 + \sqrt {127225} }}{{14}}\] thì \[\frac{{180}}{y} = \frac{{180}}{x} - 1\]\[ \approx \]6,8( giờ) ( thỏa mãn điều kiện)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
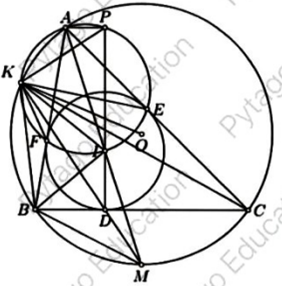
a) Do AI là tia phân giác của góc BAC nên M là điểm chính giữa cung BC không chứa A của (O) \[ \Rightarrow \]MB=MC.
Từ đó ta có biến đổi góc sau:
Do đó tam giác MBI cân tại M hay MB=MI. Mặt khác ta cũng có MB=MC. Vậy MB=MC=MI\[ \Rightarrow \]đpcm.
Gọi K là giao điểm thứ hai của (AEF) và (O). Ta sẽ chứng minh K\( \equiv \)K’. Thật vậy:
Do tứ giác AK’FE nội tiếp nên (1)
Mặt khác : ( góc nội tiếp cùng chắn cung BC của (O). (2)
Từ (1) và (2) \[ \Rightarrow \]
. Gọi K’ là giao điểm thứ hai của (AEF) và (O). Ta sẽ chứng minh K\( \equiv \)K’. Thật vậy:
Do tứ giác AK’FE nội tiếp nên (1)
Mặt khác : ( góc nội tiếp cùng chắn cung BC của (O). (2)
Từ (1) và (2) \[ \Rightarrow \]
Mặt khác:
Từ đó suy ra
\[ \Rightarrow \]K’D là phân giác của góc BK’C.
Mà M cũng chính là điểm chính giữa cung BC không chứa K’ của (O) \[ \Rightarrow \]K’, D, M thẳng hang.
Vậy K\( \equiv \)K’.
b) Xét hai tam giác MBD và MKB, ta có:
Xét hai tam giác MID và MKI, ta có:
Ta có: . Mà \[AP\parallel BC \Rightarrow PI \bot BC.\]
Mặt khác : \[ID \bot BC.\]Từ đó suy ra P,I,D thẳng hàng.
Từ (3) và (4) hay \[KP \bot KM.\]
Lời giải
Kí hiệu (i;j) là sau khi gieo một con xúc sắc cân đối và đồng chất hai lần lien tiếp ta được lần thứ nhất xuất hiện mặt có số chấm là i, lần thứ hai xuất hiện mặt có số chấm là j (với i,j \[ \in \]{1;2;…;6})
\[ \Rightarrow \]Không gian mẫu \[\Omega \] ={(1;1), (1;2), (1;3), (1;4), (1;5), (1;6), (2;1) , (2;2) , (2;3) , (2;4) , (2;5) , (2;6), (3;1) , (3;2) , (3;3) , (3;4) , (3;5) , (3;6), (4;1) , (4;2) , (4;3 ), (4;4 ), (4;5), (4;6), (5;1) , (5;2) , (5;3) , (5;4) , (5;5) , (5;6), (6;1) , (6;2) , (6;3) , (6;4) , (6;5) , (6;6)}.
\[ \Rightarrow \]Số phần tử của không gian mẫu n(\[\Omega \])=36
Gọi A là biến cố: “Tổng số chấm trên mặt xuất hiện của con xúc sắc trong hai lần gieo không lớn hơn 6”
\[ \Rightarrow \]A={(1;1), (1;2), (1;3), (1;4), (1;5), (2;1) , (2;2) , (2;3) , (2;4) , (3;1) , (3;2) , (3;3), (4;1) , (4;2), (5;1)}
\[ \Rightarrow \]Số phần tử của A là n(A)=15
Vậy số xác suất cần tìm là P(A)= \[\frac{{n(A)}}{{n(\Omega )}} = \frac{{15}}{{36}} = \frac{5}{{12}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.