a) Cho các số nguyên \(a,b,c,d\) thỏa mãn điều kiện \({a^3} + {b^3} - 8{c^3} + 28{d^3} = 0.\) Chứng minh rằng \({\left( {a + b + c + d} \right)^2}\) chia hết cho 9.
b) Chứng minh rằng tồn tại đa thức \(P\left( x \right)\) có hệ số thực, bậc 2024 thỏa mãn điều kiện \(P\left( {{x^2} - 2} \right)\) chia hết cho \(P\left( x \right)\).
Quảng cáo
Trả lời:
a) Ta có: \({a^3} + {b^3} - 8{c^3} + 28{d^3} = 0 \Rightarrow {a^3} + {b^3} + {c^3} + {d^3} \vdots 3\)
\( \Rightarrow {\left( {a + b} \right)^3} - 3ab\left( {a + b} \right) + {\left( {c + d} \right)^3} - 3cd\left( {c + d} \right) \vdots 3\)
\( \Rightarrow {\left( {a + b} \right)^3} + {\left( {c + d} \right)^3} \vdots 3\)
\( \Rightarrow {\left( {a + b + c + d} \right)^3} - 3\left( {a + b} \right)\left( {c + d} \right)\left( {a + b + c + d} \right) \vdots 3\)
\( \Rightarrow {\left( {a + b + c + d} \right)^3} \vdots 3\)
\( \Rightarrow a + b + c + d \vdots 3\)
\( \Rightarrow {\left( {a + b + c + d} \right)^2} \vdots 9\) (đpcm)
b) Xét đa thức \(P\left( x \right) = a{\left( {x + 1} \right)^{1012}}{\left( {x - 2} \right)^{1012}}\), với \(a \in \mathbb{R}\), đa thức \(P\left( x \right)\) có bậc là 2024
Ta có:
\(P\left( {{x^2} - 2} \right) = a.{\left( {{x^2} - 1} \right)^{1012}}{\left( {{x^2} - 4} \right)^{1012}} = a{\left( {x + 1} \right)^{1012}}{\left( {x - 2} \right)^{1012}}{\left( {x - a} \right)^{1012}}{\left( {x + 2} \right)^{1012}}\)
\( = P\left( x \right){\left( {x - 1} \right)^{1012}}{\left( {x + 2} \right)^{1012}}\)
\( \Rightarrow P\left( {{x^2} - 2} \right)\) chia hết cho đa thức \(P\left( x \right)\)
Vậy tồn tại đa thức \(P\left( x \right) = a{\left( {x + 1} \right)^{1012}}{\left( {x - 2} \right)^{1012}}\) với hệ số thức, có bậc 2024 thỏa mãn đã thức \(P\left( {{x^2} - 2} \right)\) chia hết cho đa thức \(P\left( x \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
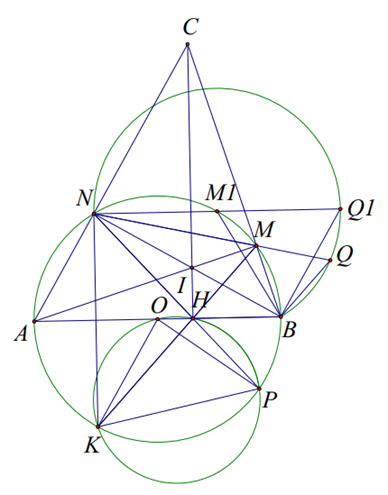
AM cắt BN tại I => I là trực tâm \(CI \bot AB\;\)
\( \Rightarrow AI \bot CB \Rightarrow B,M,C\) thẳng hàng.
Dễ thấy \(\Delta BCH \sim \Delta ICM \Rightarrow CB.CM = CI.CH\)
Dễ thấy \(\widehat {NHI} = \widehat {MHI} = \widehat {MBI} = \widehat {IAN} \Rightarrow \widehat {NHA} = \widehat {BHM}\)
Mà \(\widehat {NHA} = \widehat {KHA}\) tính chất đối xứng
\( \Rightarrow \widehat {AHK} = \widehat {BHM}\) mà \(\widehat {BHM} + \widehat {MHA} = {90^0}\)
\( \Rightarrow \widehat {AHK} + \widehat {AHM} = {180^0}\) suy ra K, H, M thẳng hàng.
b) Ta có \(\widehat {PHK} = 2.\widehat {PNK}\) (góc ngoài \(\Delta HNK\) cân)
\(\widehat {KOP} = 2\widehat {KNP}\) góc nội tiếp
\( \Rightarrow \) Tứ giác \(KOHP\) nội tiếp vì N cố định suy ra OK cố định. Vậy tâm đường tròn ngoại tiếp tam giác KHP thuộc trung trực OK.
c) Ta có \(\widehat {NMB} = {120^0}\). Trên tia đối MN lấy Q sao cho \(MB = MQ \Rightarrow \widehat {NQB} = {60^0}\)
NB cố định \( \Rightarrow Q\) thuộc cung chứa góc \({60^0}\) dựng trên NB \( \Rightarrow MN + MB\) lớn nhất khi \(NQ\) là đường kính của đường tròn
\(MB = MQ = MN \Rightarrow M \equiv M1,\;Q \equiv Q1\).
Vậy M là trung điểm cung \(NB \Rightarrow MN + MB\) lớn nhất \(MN + NB = 2R\)
Lời giải
Ta có \(\left( {a\sqrt {{a^2} + 9bc} + b\sqrt {{b^2} + 9ac} + c\sqrt {{c^2} + 9ab} } \right).F \ge {\left( {a + b + c} \right)^2}\)
Đặt \(Q = a\sqrt {{a^2} + 9bc} + b\sqrt {{b^2} + 9ac} + c\sqrt {{c^2} + 9ab} \)
\({Q^2} = {\left[ {\sqrt a \sqrt {{a^3} + 9ac} + \sqrt b \sqrt {{b^3} + 9ac} + \sqrt c \sqrt {{c^3} + 9ab} } \right]^2} \le \left( {a + b + c} \right)\left( {{a^3} + {b^3} + {c^3} + 27abc} \right)\)
Ta lại có \({a^3} + {b^3} + {c^3} = {\left( {a + b + c} \right)^3} - 3\left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) \le {\left( {a + b + c} \right)^3} - 24abc\)
\( \Rightarrow \left( {a + b + c} \right)\left( {{a^3} + {b^3} + {c^3} + 27abc} \right) \le \left( {a + b + c} \right)\left[ {{{\left( {a + b + c} \right)}^3} + 3abc} \right]\) mà \(3abc \le \) \(\frac{{{{\left( {a + b + C} \right)}^3}}}{9}\)
\( \Rightarrow \left( {a + b + c} \right)\left( {{a^3} + {b^3} + {c^3} + 27abc} \right) \le \frac{{10{{\left( {a + b + c} \right)}^4}{\rm{\;\;}}}}{9}\)
\( \Rightarrow Q \le \frac{{\sqrt {10} {{\left( {a + b + c} \right)}^2}}}{3}\;\)mà \(\left( {a\sqrt {{a^2} + 9bc} + b\sqrt {{b^2} + 9ac} + c\sqrt {{c^2} + 9ab} } \right).F \ge {\left( {a + b + c} \right)^2}\)
Suy ra \(F \ge \) \(\frac{{3\sqrt {10} }}{{10}}\). Vậy min F = \(\frac{{3\sqrt {10} }}{{10}}\).
Dấu “=” xảy ra \( \Leftrightarrow a = b = c\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.