Trong không gian với hệ tọa độ \(Oxyz\), một cabin cáp treo xuất phát từ điểm \(A\left( {10;3;0} \right)\) và chuyển động đều theo đường cáp có vectơ chỉ phương là \(\overrightarrow u = \left( {2; - 2;1} \right)\) với tốc độ \(4,5\;{\rm{m/s}}\) (đơn vị trên mỗi trục tọa độ là mét).

Giả sử cabin dừng ở điểm B có hoành độ \({x_B} = 550\). Khi đó quãng đường AB dài bao nhiêu mét?
Trong không gian với hệ tọa độ \(Oxyz\), một cabin cáp treo xuất phát từ điểm \(A\left( {10;3;0} \right)\) và chuyển động đều theo đường cáp có vectơ chỉ phương là \(\overrightarrow u = \left( {2; - 2;1} \right)\) với tốc độ \(4,5\;{\rm{m/s}}\) (đơn vị trên mỗi trục tọa độ là mét).

Giả sử cabin dừng ở điểm B có hoành độ \({x_B} = 550\). Khi đó quãng đường AB dài bao nhiêu mét?
Quảng cáo
Trả lời:
Đáp án:
Trả lời: 810
Phương trình đường cáp là: \(\left\{ \begin{array}{l}x = 10 + 2t\\y = 3 - 2t\\z = t\end{array} \right.\).
Vì cabin dừng ở điểm B có hoành độ \({x_B} = 550\) nên \(10 + 2t = 550 \Leftrightarrow t = 270\).
Do đó \(B\left( {550; - 537;270} \right)\).
Khi đó \(AB = \sqrt {{{\left( {550 - 10} \right)}^2} + {{\left( { - 537 - 3} \right)}^2} + {{270}^2}} = 810\)m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: 4,5
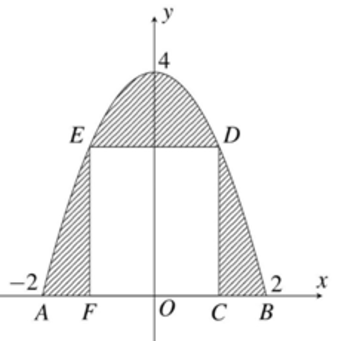
Vì chiều cao của cổng bằng 4 m nên \(\left( P \right):y = a{x^2} + 4\).
Mà \(\left( {2;0} \right) \in \left( P \right)\) nên \(0 = a{.2^2} + 4 \Leftrightarrow a = - 1\). Do đó \(y = - {x^2} + 4\).
Do đó diện tích toàn bộ chiếc cổng là \(S = \int\limits_{ - 2}^2 {\left| { - {x^2} + 4} \right|} dx = \frac{{32}}{3}\).
Vì \(D \in \left( P \right)\) nên \(D\left( {a; - {a^2} + 4} \right),\left( {0 < a < 2} \right)\).
Suy ra \(FC = 2a;CD = 4 - {a^2}\). Do đó \({S_{CDEF}} = 2a.\left( {4 - {a^2}} \right) = 8a - 2{a^3}\).
Để chi phí phần trang trí là nhỏ nhất thì diện tích phần tô màu phải nhỏ nhất hay diện tích hình chữ nhật \(CDEF\) phải lớn nhất.
Xét hàm số \(f\left( a \right) = 8a - 2{a^3}\). Có \(f'\left( a \right) = 8 - 6{a^2} = 0 \Leftrightarrow a = \frac{{2\sqrt 3 }}{3}\) vì \(0 < a < 2\).
Bảng biến thiên
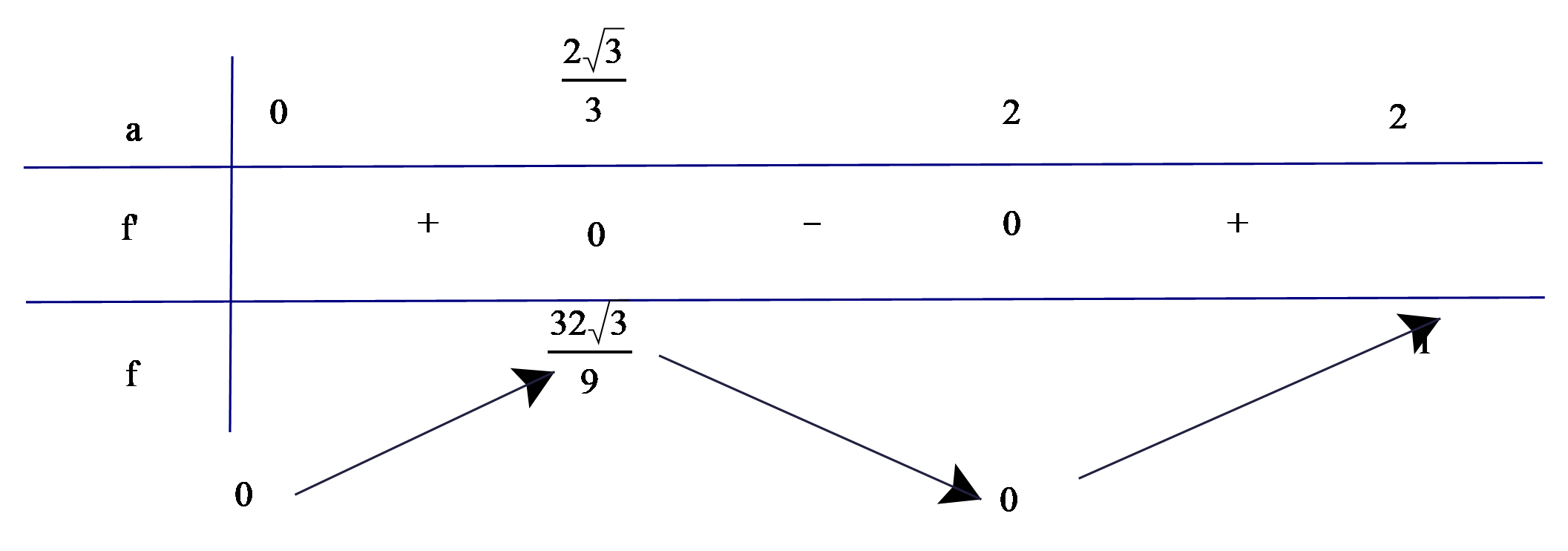
Từ bảng biến thiên ta có diện tích \(CDEF\) lớn nhất bằng \(\frac{{32\sqrt 3 }}{9}\) khi \(a = \frac{{2\sqrt 3 }}{3}\).
Khi đó diện tích phần tô màu là \({S_1} = S - {S_{CDEF}} = \frac{{32}}{3} - \frac{{32\sqrt 3 }}{9}\).
Chi phí tối thiểu là: \(\left( {\frac{{32}}{3} - \frac{{32\sqrt 3 }}{9}} \right).1000000 \approx 4,5\) triệu đồng.
Lời giải
Trả lời: 1309
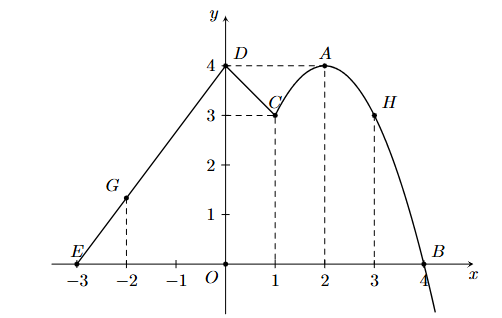
Vì hàm số bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) có đồ thị là một parabol (P) có đỉnh \(S\left( {1; - 2} \right)\) và cắt trục tung tại điểm có tung độ bằng 1 nên ta có
.Suy ra
Có \(F\left( x \right) = \int {\left( {3{x^2} - 6x + 1} \right)dx} = {x^3} - 3{x^2} + x + C\).
Mà \(F\left( 0 \right) = 1\) nên \(C = 1\). Do đó \(F\left( x \right) = {x^3} - 3{x^2} + x + 1\).
Đồ thị hàm số \(y = F\left( x \right)\) đi qua điểm \(M\left( {12;m} \right)\) nên \({12^3} - {3.12^2} + 12 + 1 = m \Leftrightarrow m = 1309\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.