Kim tự tháp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của pharaoh Khufu. Được xây dựng vào đầu thế kỷ 26 trước Công nguyên trong khoảng thời gian 27 năm, đây là kim tự tháp lâu đời nhất còn nằm trong Bảy kỳ quan của thế giới cổ đại, và là kim tự tháp duy nhất với phần lớn còn nguyên vẹn. Kim tự tháp này được xây dựng theo mô hình là hình chóp tứ giác đều với kích thước như sau: chiều cao xấp xỉ \(138{\rm{m}}\), độ dài đáy xấp xỉ \(230\,{\rm{m}}\) (theo số liệu mới nhất trên https://vi.wikipedia.org/wiki/). Tính khoảng cách từ tâm của đáy kim tự tháp đến mặt bên.
Kim tự tháp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của pharaoh Khufu. Được xây dựng vào đầu thế kỷ 26 trước Công nguyên trong khoảng thời gian 27 năm, đây là kim tự tháp lâu đời nhất còn nằm trong Bảy kỳ quan của thế giới cổ đại, và là kim tự tháp duy nhất với phần lớn còn nguyên vẹn. Kim tự tháp này được xây dựng theo mô hình là hình chóp tứ giác đều với kích thước như sau: chiều cao xấp xỉ \(138{\rm{m}}\), độ dài đáy xấp xỉ \(230\,{\rm{m}}\) (theo số liệu mới nhất trên https://vi.wikipedia.org/wiki/). Tính khoảng cách từ tâm của đáy kim tự tháp đến mặt bên.
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 2 Toán 11 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
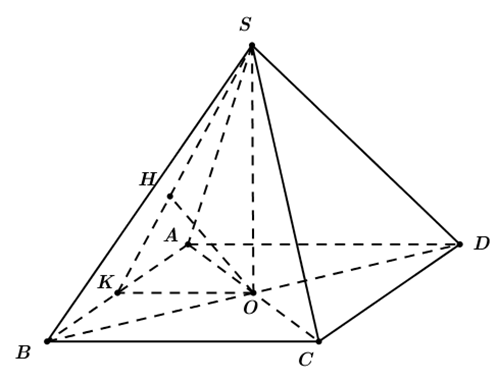
Ta có mô hình kim tự tháp như hình vẽ, là hình chóp tứ giác đều \(S.ABCD\).
Gọi \(O = BD \cap AC \Rightarrow SO \bot \left( {ABCD} \right)\), \(K\) là trung điểm \(AB\).
Vì \(O,K\)là trung điểm của \(BD,AB\) \( \Rightarrow OK\)là đường trung bình của \(\Delta BAD\).
Suy ra \(OK{\rm{//}}AD\) mà \(AD \bot AB \Rightarrow OK \bot AB\).
Kẻ \(OH \bot SK\) tại \(H\).
Ta có:
\(\left\{ \begin{array}{l}AB \bot OK\\AB \bot SO\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow AB \bot \left( {SOK} \right) \Rightarrow AB \bot OH\).
Vì \(\left\{ \begin{array}{l}OH \bot AB\\OH \bot SK\end{array} \right. \Rightarrow OH \bot \left( {SAB} \right) \Rightarrow d\left( {O,\left( {SAB} \right)} \right) = OH\).
Theo đề, có \(SO = 138{\rm{m;}}AD = 230{\rm{m}} \Rightarrow OK = 115{\rm{m}}\)
Xét \(\Delta SOK\) vuông tại \(O\), có: \(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{K^2}}} = \frac{1}{{{{138}^2}}} + \frac{1}{{{{115}^2}}} = \frac{{61}}{{476100}}\).
\( \Rightarrow OH \approx 88,35\,{\rm{m}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Ta có \[v\left( t \right) = s'\left( t \right) = - 3{t^2} + 18t + 1 = - 3\left( {{t^2} - 6t + 9 - 9} \right) + 1 = - 3{\left( {t - 3} \right)^2} + 28 \le 28\].
Vậy giá trị lớn nhất của vận tốc chất điểm là 28 m/s đạt được khi \(t = 3\left( {\rm{s}} \right)\).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có \({3^{4 - {x^2}}} \ge 27\)\( \Leftrightarrow {3^{4 - {x^2}}} \ge {3^3}\)\( \Leftrightarrow 4 - {x^2} \ge 3\)\( \Leftrightarrow {x^2} \le 1 \Leftrightarrow - 1 \le x \le 1\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập