Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập số thực \(\mathbb{R}\)?
Quảng cáo
Trả lời:
Đáp án đúng là: A
Xét từng đáp án:
+) Hàm số \(y = {\left( {\frac{2}{e}} \right)^x}\) có tập xác định \(\mathbb{R}\) và có cơ số \(0 < \frac{2}{e} < 1\) nên hàm số này nghịch biến trên \(\mathbb{R}\).
+) Hàm số \(y = {\left( {\frac{\pi }{3}} \right)^x}\) có tập xác định \(\mathbb{R}\) và có cơ số \(\frac{\pi }{3} > 1\) nên hàm số này đồng biến trên \(\mathbb{R}\).
+) Hàm số \(y = {\log _\pi }\left( {4{x^2} + 1} \right)\) có tập xác định \(\mathbb{R}\) (do \(4{x^2} + 1 > 0,\,\forall x \in \mathbb{R}\)) và có cơ số \(\pi > 1\) nên hàm số này đồng biến trên \(\mathbb{R}\).
+) Hàm số \(y = {\log _{\frac{1}{3}}}x\) có tập xác định \(\left( {0;\, + \infty } \right)\) và có cơ số \(0 < \frac{1}{3} < 1\) nên hàm số này nghịch biến trên \(\left( {0;\, + \infty } \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
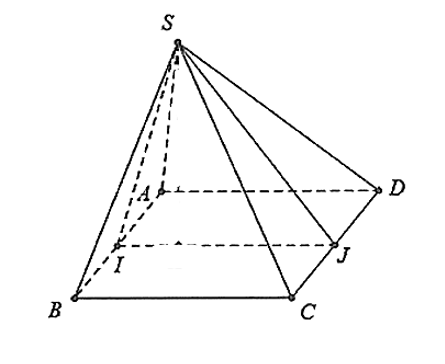
a) Ta có tam giác \(SAB\) đều cạnh \(a\) nên \(SI = \frac{{a\sqrt 3 }}{2}\).
Tứ giác \(IBCJ\) là hình chữ nhật nên \(IJ = BC = a\).
Tam giác \(SCD\) là tam giác vuông cân đỉnh \(S\) nên \(SJ = \frac{{CD}}{2} = \frac{a}{2}\).
Do đó, \(S{J^2} + S{I^2} = I{J^2}\,\,\left( { = {a^2}} \right)\), suy ra tam giác \(SIJ\) vuông tại \(S\).
Vậy \(SI \bot SJ\).
b) Vì tam giác \(SCD\) là tam giác cân đỉnh \(S\) nên \(SJ \bot CD\).
Do \(AB\,{\rm{//}}\,CD\) nên \(SJ \bot AB\) mà \(SI \bot SJ\) nên \(SJ \bot \left( {SAB} \right)\).
Chứng minh tương tự ta có \(SI \bot \left( {SCD} \right)\).
Câu 2
Lời giải
Đáp án đúng là: B
Ta có \({\log _9}10 = {\log _{{3^2}}}\left( {2 \cdot 5} \right) = \frac{1}{2}{\log _3}\left( {2 \cdot 5} \right) = \frac{1}{2}\left( {{{\log }_3}2 + {{\log }_3}5} \right)\).
Áp dụng công thức đổi cơ số ta có \({\log _2}3 = \frac{{{{\log }_3}3}}{{{{\log }_3}2}} = \frac{1}{{{{\log }_3}2}}\), suy ra \({\log _3}2 = \frac{1}{{{{\log }_2}3}} = \frac{1}{a}\).
Tương tự \({\log _2}5 = \frac{{{{\log }_3}5}}{{{{\log }_3}2}} \Rightarrow {\log _3}5 = {\log _2}5 \cdot {\log _3}2 = b \cdot \frac{1}{a} = \frac{b}{a}\).
Do đó, \({\log _9}10 = \frac{1}{2}\left( {\frac{1}{a} + \frac{b}{a}} \right) = \frac{{1 + b}}{{2a}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
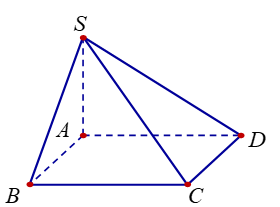
![Cho hình lập phương \[ABCD.A'B'C'D'\] (tham khảo hình vẽ bên dưới). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/12/23-1766721502.png)