Cho phương trình: \({x^2} - 2(m + 1)x + {m^2} + m = 0\) với m là tham số.

1) Tìm các giá trị của tham số m để phương trình đã cho có hai nghiệm phân biệt \({x_1},\,{x_2}\).

2) Tìm hệ thức liên hệ giữa \({x_1}\) và \({x_2}\) mà không phụ thuộc vào tham số m.

1) Ta có CH ^ BD Þ H nhìn CD dưới một góc vuông (1)

Theo tính chất hai tiếp tuyến cắt nhau CD và BD, ta có DC = DB

Hai bán kính OC = OB

Þ OD là trung trực của BC Þ OD ^ CB

Þ N nhìn CD dưới một góc vuông (2)

Từ (1) và (2) Þ tứ giác CNHD nội tiếp được trong đường tròn.

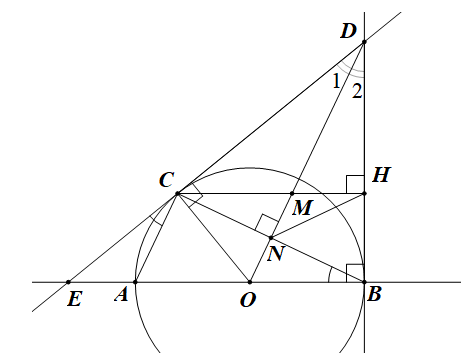
2) Theo tính chất hai tiếp tuyến cắt nhau CD và BD, ta có DC = DB, ta có \(\widehat {{D_1}} = \widehat {{D_2}}\)

Theo tính chất tiếp tuyến và giả thiết, ta có góc \(\widehat {COD} = \widehat {DMH}\) (cùng phụ với hai góc bằng nhau\(\widehat {{D_1}} = \widehat {{D_2}}\))

Mặt khác \(\widehat {DMH} = \widehat {CMO}\) (đối đỉnh) Þ \(\widehat {COD} = \widehat {CMO}\)

DCOM có \(\widehat {COM} = \widehat {CMO}\) Þ cân tại C Þ \(CM = CO\).

3) DEAC và DECB có góc E chung và góc \(\widehat {ECA} = \widehat {CBA}\) (cùng chắn cung AC)

Þ đồng dạng Þ \(\frac{{EA}}{{EC}} = \frac{{EC}}{{EB}} \Rightarrow EA.EB = E{C^2}\).

4) Hình nón được tạo bởi tam giác vuông DNB quay quanh DN

Þ bán kính \(r = NB\) và chiều cao \(h = ND\).

Theo Pitago cho tam giác vuông BOD: \(OD = \sqrt {O{B^2} + B{D^2}}  = \sqrt {36 + 64}  = 10cm\).

Theo hệ thức lượng trong tam giác vuông BOD, ta có: \(BN.OD = OB.BD \Rightarrow BN = \frac{{6.8}}{{10}} = 4,8cm\).

Và \(B{D^2} = DN.DO \Rightarrow DN = \frac{{64}}{{10}} = 6,4cm\)

Thể tích của hình nón tạo thành \(V = \frac{1}{3}\pi .{r^2}.h = \frac{1}{3}\pi .{(4,8)^2}.6,4 = \frac{{6144}}{{125}}\pi  \approx 154,4156\,\left( {c{m^3}} \right)\).

Gọi giá tiền niêm yết (khi chưa giảm giá) của một cái quạt máy và một ấm đun siêu tốc là \(x,\,y\,\left( {x > 0,\,y > 0} \right)\) (đồng).

Ta có phương trình \(x + y = 630000\).

Giá tiền quạt máy sau khi giảm giá là \(x - 15\% x = 85\% x = 0,85x\).

Giá tiền ấm siêu tốc sau khi giảm giá là \(y - 12\% y = 88\% y = 0,88y\).

Ta có phương trình \(0,85x + 0,88y = 543000\).

Giải hệ \(\left\{ \begin{array}{l}x + y = 630000\\0,85x + 0,88y = 543000\end{array} \right.\)

\(\left\{ \begin{array}{l}x + y = 630000\\0,85x + 0,88y = 543000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0,88x + 0,88y = 554400\\0,85x + 0,88y = 543000\end{array} \right. \Leftrightarrow \) \(\left\{ \begin{array}{l}0,03x = 11400\\x + y = 630000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 380000\\380000 + y = 630000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 380000\\y = 250000\end{array} \right.\)

Vậy giá tiền niêm yết (khi chưa giảm giá) của một cái quạt máy và một ấm đun siêu tốc là 380000 (đồng) và 250000 (đồng).