Cho \(a,b,c\)là các số thực dương. Chứng minh rằng: \({a^2} + {b^2} + 2abc + {c^2} + 1 \ge 2\left( {ab + ac + bc} \right)\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét ba \(a - 1;b - 1;c - 1\) số luôn có hai số cùng dấu.
Giả sử \(a - 1;b - 1\) là hai số cùng dâu, suy ra \(\left( {a - 1} \right)\left( {b - 1} \right) \ge 0\)
\( \Rightarrow c\left( {a - 1} \right)\left( {b - 1} \right) \ge 0\)
\( \Rightarrow abc - ac - bc + c \ge 0\)
\( \Rightarrow 2abc + 2c \ge 2ac + 2bc\) (1)
Lại có \({\left( {c - 1} \right)^2} \ge 0 \Rightarrow {c^2} - 2c + 1 \ge 0\) (2)
Từ (1), (2) ta có \(2abc + {c^2} + 1 \ge 2ac + 2bc\)
Suy ra \({a^2} + {b^2} + 2abc + {c^2} + 1 \ge 2ab + 2ac + 2bc\) (đpcm)
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
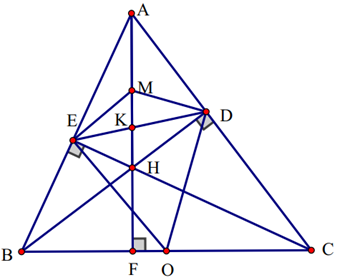
1) Vì \(BD,CE\) là đường cao nên \(\widehat {BDA} = \widehat {CEA} = 90^\circ \)
Tứ giác \(ADHE\) có \(\widehat {HDA} + \widehat {HEA} = 90^\circ + 90^\circ = 180^\circ \) nên \(ADHE\) nội tiếp đường tròn, suy ra \(\widehat {DAH} = \widehat {DEH}\) (hai góc nội tiếp cùng chắn cung \(HE\))
Vậy \(\widehat {DAH} = \widehat {DEH}\).
2) Tam giác \(ADH\) vuông tại \(D\) có \(DM\) là trung tuyến (là trung điểm \(AH\)), suy ra \(MD = MA = MH = \frac{{AH}}{2}\)
Tương tự: \(ME = MA = MH = \frac{{AH}}{2}\)
Suy ra \(MD = MA = MH = ME\) \( \Rightarrow \Delta MAD\) cân tại \(M\), suy ra \(\widehat {MDA} = \widehat {MAD}\).
Tương tự: \(\widehat {ODC} = \widehat {OCD}\)
Do đó: \(\widehat {MDA} + \widehat {ODC} = \widehat {MAD} + \widehat {OCD} = 90^\circ \)
Suy ra \(\widehat {MDO} = 90^\circ \)
Tương tự: \(\widehat {MEO} = 90^\circ \)
Tứ giác \(MDOE\) có \(\widehat {MDO} + \widehat {MEO} = 90^\circ + 90^\circ = 180^\circ \) nên \(MDOE\) nội tiếp đường tròn.
3) Ta có \(A{H^2} = 2MK.\left( {AF + HF} \right)\) (1)
\( \Leftrightarrow A{H^2} = 2MK.\left( {AH + HF + HF} \right)\)
\( \Leftrightarrow 4M{H^2} = 2MK.\left( {2HM + 2HF} \right)\)
\( \Leftrightarrow M{H^2} = MK.HM + MK.HF\)
\( \Leftrightarrow M{H^2} - MK.HM = MK.HF\)
\( \Leftrightarrow MH.\left( {MH - MK} \right) = MK.HF\)
\( \Leftrightarrow MH.HK = MK.HF\)
Tam giác \(DKM\) đồng dạng với tam giác \(FDM\) suy ra \(\frac{{MK}}{{MD}} = \frac{{DK}}{{DH}}\) (2)
Vì (2) được chứng minh nên (1) được chứng minh.
Vậy \(A{H^2} = 2MK.\left( {AF + HF} \right)\).
Lời giải
1) Với \(x > 0,x \ne 1\) ta có \(A = \sqrt x .\left( {\frac{1}{{x - \sqrt x }} + \frac{1}{{\sqrt x - 1}}} \right):\frac{{\sqrt x + 1}}{{x - 2\sqrt x + 1}}\)
\(A = \sqrt x .\left[ {\frac{1}{{\sqrt x \left( {\sqrt x - 1} \right)}} + \frac{1}{{\sqrt x - 1}}} \right]:\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}\)
\(A = \sqrt x .\frac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}:\frac{{\sqrt x + 1}}{{{{\left( {\sqrt x - 1} \right)}^2}}}\)
\(A = \frac{{1 + \sqrt x }}{{\sqrt x - 1}}.\frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x + 1}}\)
\(A = \sqrt x - 1\)
Vậy \(A = \sqrt x - 1\) với \(x > 0,x \ne 1\).
2) Ta có \(\left( d \right)\) song song với \(\left( {d'} \right)\) \( \Rightarrow \left\{ \begin{array}{l}a = 5\\b \ne 3\end{array} \right.\)
Lại có \(\left( d \right)\) đi qua \(A\left( {1;3} \right)\) \( \Rightarrow 3 = 1.a + b\)
\( \Rightarrow 3 = 1.5 + b\) \( \Leftrightarrow b = - 2\)
Vậy \(a = 5,b = - 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập