Người ta thả vào cốc \(6\) viên bi hình cầu giống hệt nhau thì thấy mực nước trong cốc dâng lên \(5\,cm\) (và nước vẫn chưa đầy cốc). Tính bán kính của mỗi viên bi.

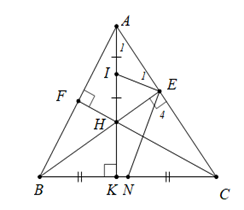
a) Chứng minh bốn điểm \(A\), \(E\), \(H\), \(F\) nằm trên cùng một đường tròn.

Ta có \[\widehat {AEB} = 90^\circ \](do \(BE\) là đường cao của \(\Delta ABC\)) hay \[\widehat {AEH} = 90^\circ \]

\[\widehat {AFC} = 90^\circ \] (do \(CF\) là đường cao của \(\Delta ABC\)) hay \[\widehat {AFH} = 90^\circ \]

Suy ra bốn điểm \(A,E,H,F\) cùng nằm trên một đường tròn đường kính \(AH\) (đpcm)

b) Chứng minh \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\);

Vì \(I\) là trung điểm của đoạn thẳng \(AH\) nên \(I\) là tâm đường tròn đường kính \(AH\)

Suy ra \(IA = IE\)

Vì\(\Delta IAE\) cân tại \(I\) nên \({\widehat A_1} = {\widehat E_1}\)                            (1)

\[\Delta EBC\] vuông tại \[E\]có \[EN\] là đường trung trrung tuyến ứng với cạnh huyền \[BC\]

Nên \(EN = NC\,\,\,\left( { = \frac{{BC}}{2}} \right)\)

Suy ra \[\Delta ENC\] cân tại \[N\] nên \(\widehat {NCE} = \widehat {{E_4}}\)                (2)

Xét \[\Delta AKC\] vuông tại \[K\] có \[\widehat {KCA} + {\widehat A_1} = 90^\circ \] hay \[\widehat {NCE} + {\widehat A_1} = 90^\circ \]        (3)

Từ (1), (2), (3) suy ra \({\widehat E_1} + {\widehat E_4} = 90^\circ \)

Lại có  \({\widehat E_1} + {\widehat E_4} + \widehat {IEN} = 180^\circ \)  (do \(A;\;E;\;C\) thẳng hàng)

Suy ra \(90^\circ  + \widehat {IEN} = 180^\circ \)hay\(\widehat {IEN} = 90^\circ \)

Suy ra \(EN \bot EI\) tại \(E\)

Do đó \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\)  (đpcm)

c) Chứng minh \[C{I^2} - I{E^2} = CK\;.\;CB\].

Áp dụng định lí Py – Ta – Go \(\Delta CIK\) vuông tại \(K\), ta có: \(C{I^2} = C{K^2} + I{K^2}\)       

Lại có \(IA = IE = IH\) (cùng bán kính đường tròn tâm I)

Suy ra \[C{I^2} - I{E^2} = C{K^2} + I{K^2} - I{E^2}\]

\[C{I^2} - I{E^2} = C{K^2} + (IK + IE)(IK - IE)\]

\[C{I^2} - I{E^2} = C{K^2} + (IK + IE)(IK - IH)\]  \[ = C{K^2} + AK\;.\;KH\]  \(\left( 4 \right)\)

Ta lại có \[CK.CB = CK(CK + KB)\] \[ = C{K^2} + CK\;.\;KB\]   \(\left( 5 \right)\)

Xét  \(\Delta KBH\) và \(\Delta KAC\) có

\(\widehat {KBH} = \widehat {KAC}\) (\( = 90^\circ  - \widehat {ACB}\));  \[\widehat {BKH} = \widehat {AKC} = 90^\circ \]

Do đó \[\left( {g - g} \right)\]

Nên \(\frac{{KB}}{{KA}} = \frac{{KH}}{{KC}}\) suy ra\(KA\;.\;KH = KB\;.\;KC\) hay \(AK\;.\;KH = CK\;.\;KB\)                  \(\left( 6 \right)\)

Từ \[\left( 4 \right)\],\(\left( 5 \right)\) và \(\left( 6 \right)\) suy ra \[C{I^2} - I{E^2} = CK\;.\;CB\]  (đpcm)

Gọi giá nhập về của chiếc ti vi là \(x\)(đồng). Theo đề cửa hàng thu lãi \(\frac{x}{{10}}\), tức là giá đã bán là \(x + \frac{x}{{10}}\). Nếu cửa hàng tiếp tục nâng giá bán chiếc tivi đó thêm \(5\% \)giá đã bán và bớt cho khách hàng 245 000 đồng, khi đó giá bán ra là \(x + \frac{x}{{10}} + \frac{5}{{100}}\left( {x + \frac{x}{{10}}} \right) - 245000\)

Theo đề khi đó cửa hàng thu lãi là 12% của giá nhập về nên ta có phương trình :

\(x + \frac{x}{{10}} + \frac{5}{{100}}\left( {x + \frac{x}{{10}}} \right) - 24\,500 = x + \frac{{12}}{{100}}x\)

Từ đó tính được \(x = 7\,000\,000\)

Vậy giá nhập về của chiếc ti vi đó là 7 triệu đồng.