(0,5 điểm) Một chiếc đu quay có bán kính \(75\;{\rm{cm}}\), tâm của vòng quay ở độ cao \(80\;{\rm{m}}\) so với mặt đất. Thời gian thực hiện mỗi vòng quay là 30 phút. Nếu một người vào cabin ở vị trí thấp nhất của đu quay thì sau 10 phút người đó ở độ cao bao nhiêu mét so với mặt đất (giả sử đu quay quay đều)?
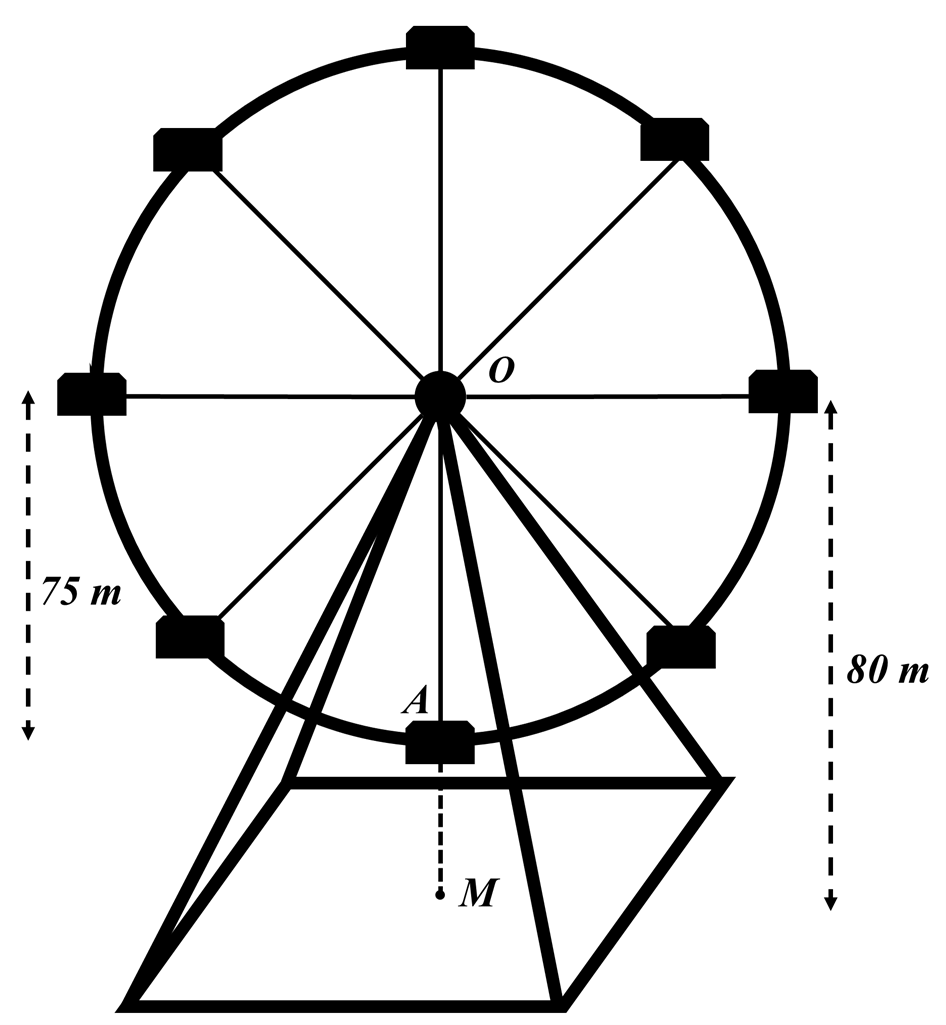
(0,5 điểm) Một chiếc đu quay có bán kính \(75\;{\rm{cm}}\), tâm của vòng quay ở độ cao \(80\;{\rm{m}}\) so với mặt đất. Thời gian thực hiện mỗi vòng quay là 30 phút. Nếu một người vào cabin ở vị trí thấp nhất của đu quay thì sau 10 phút người đó ở độ cao bao nhiêu mét so với mặt đất (giả sử đu quay quay đều)?

Quảng cáo
Trả lời:
Gọi vị trí ban đầu của người đó là điểm \(A\).
Vì thời gian thực hiện mỗi vòng của đu quay là \(30\) phút nên khi đu quay quay đều thì \(10\) phút người đó đi được \(\frac{1}{3}\) vòng tròn và đang ở vị trí điểm B như hình vẽ sau:
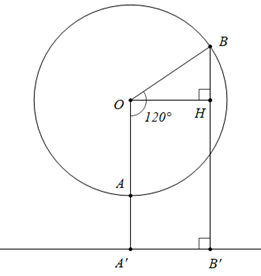
Gọi \(A',\,B'\) lần lượt là hình chiếu của \(A,\,B\) trên mặt đất, kẻ \(OH \bot BB'\).
Ta có: \(\widehat {AOB} = \frac{1}{3}\; \cdot \;{360^ \circ } = {120^ \circ },\,\)\(OA' = 80\;{\rm{m}}\).
Vì \(OA'B'H\) là hình chữ nhật (tứ giác có \(3\) góc vuông) nên \(HB' = OA' = 80\,\;\left( {\rm{m}} \right)\)
Ta có: \(\widehat {AOH} = {90^ \circ }\) suy ra \(\widehat {BOH} = {120^ \circ } - {90^ \circ } = {30^ \circ }\)
Xét tam giác vuông \(OBH\) có: \(BH = OB.\sin {30^ \circ } = 75\; \cdot \;\frac{1}{2} = 37,5\,\left( m \right)\)
Mà \(BB' = BH + HB' = 37,5 + 80 = 117,5\;\,\left( {\rm{m}} \right)\).
Vậy sau \(10\) phút người đó ở độ cao \(117,5\;{\rm{m}}\) so với mặt đất.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi giá nhập về của chiếc ti vi là \(x\)(đồng). Theo đề cửa hàng thu lãi \(\frac{x}{{10}}\), tức là giá đã bán là \(x + \frac{x}{{10}}\). Nếu cửa hàng tiếp tục nâng giá bán chiếc tivi đó thêm \(5\% \)giá đã bán và bớt cho khách hàng 245 000 đồng, khi đó giá bán ra là \(x + \frac{x}{{10}} + \frac{5}{{100}}\left( {x + \frac{x}{{10}}} \right) - 245000\)
Theo đề khi đó cửa hàng thu lãi là 12% của giá nhập về nên ta có phương trình :
\(x + \frac{x}{{10}} + \frac{5}{{100}}\left( {x + \frac{x}{{10}}} \right) - 24\,500 = x + \frac{{12}}{{100}}x\)
Từ đó tính được \(x = 7\,000\,000\)
Vậy giá nhập về của chiếc ti vi đó là 7 triệu đồng.
Lời giải
Gọi \[R\] là bán kính viên bi. Thể tích \(6\) viên bi là thể tích nước dâng lên trong cốc. Khi đó thể tích \(6\) viên bi là \({V_2} = 6.\frac{4}{3}\pi .{R^3} = 8\pi .{R^3}\)
Từ đó: \(8\pi .{R^3} = 125\pi \Leftrightarrow R = \frac{5}{2}\) (cm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.