a)  Rút gọn biểu thức \[A = \sqrt 9  - 2\].

b) Giải phương trình \[2x - 6 = 0\].

c)  Cho hàm số \(y = f\left( x \right) = 3{x^2}\). Tính giá trị hàm số tại \(x = 2\).

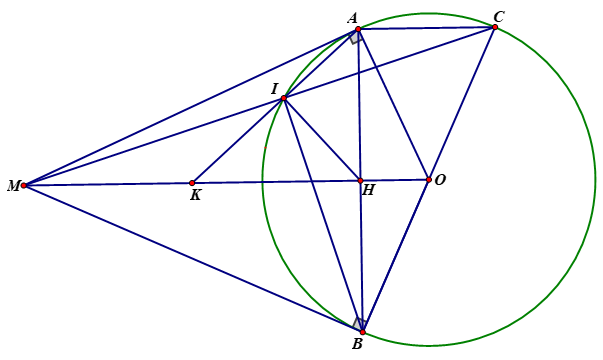
a) Xét tứ giác MAOB có

\(\widehat {MAO} + \widehat {MBO} = {90^0} + {90^0} = {180^0}\)

Nên tứ giác MAOB nội tiếp đường tròn đường kính MO

b) Xét (O) có MA, MB là 2 tiếp tuyến cắt nhau tại M

Nên MA = MB

Lại có : OA = OB (= R)

Do đó: MO là đường trung trực của AB

Suy ra: \({\rm{MO }} \bot {\rm{ AB}}\)

Xét \({\rm{\Delta MAI}}\)và \({\rm{\Delta MCA}}\)có:

\(\widehat {{\rm{AMI}}}\)chung

\(\widehat {{\rm{MAI}}}{\rm{ = }}\widehat {{\rm{ACM}}}\)(góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AI)

Do đó: \({\rm{\Delta MAI }} \sim {\rm{ }}\Delta {\rm{MCA}}\)

\(\begin{array}{l} \Rightarrow \frac{{MA}}{{MC}} = \frac{{MI}}{{MA}}\\ \Rightarrow M{A^2} = MI.MC\left( 1 \right)\end{array}\)

Áp dụng hệ thức lượng vào tam giác MAO vuông tại A, đường cao AH ta có

\(M{A^2} = MH.MO\left( 2 \right)\)

Từ (1), (2) suy ra: \(MI.MC = MH.MO\)

Xét \({\rm{\Delta MHI}}\)và \({\rm{\Delta MCO}}\)có:

\(\widehat {{\rm{OMC}}}\)chung

\(\frac{{MI}}{{MH}} = \frac{{MO}}{{MC}}\)(vì MI.MC = MH.MO)

Do đó: \({\rm{\Delta MHI }} \sim {\rm{ }}\Delta {\rm{MCO}}\)

\( \Rightarrow \widehat {MHI} = \widehat {MCO}\)

Mà \(\widehat {MCO} = \widehat {IAH}\)(2 góc nội tiếp cùng chắn cung IB)

Nên \(\widehat {MHI} = \widehat {IAH}\)

Ta có: \(\widehat {IHM} + \widehat {IHA} = {90^0}\)

Mà \(\widehat {MHI} = \widehat {IAH}\)

Nên \(\widehat {IAH} + \widehat {IHA} = {90^0}\)

Do đó tam giác AIH vuông tại I

Vậy: \(AK \bot IH\)

c) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta có

\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow AB = 4\sqrt 3 \left( {cm} \right)\end{array}\)

Xét \({\rm{\Delta ABC}}\)vuông tại A, ta có

\(\begin{array}{l}\sin \widehat {ABC} = \frac{{AC}}{{BC}} = \frac{1}{2}\\ \Rightarrow \widehat {ABC} = {30^0}\end{array}\)

\( \Rightarrow \widehat {MBH} = {90^0} - {30^0} = {60^0}\)

Xét tam giác MAB cân tại M có

\(\widehat {MBH} = {60^0}\)

Nên tam giác MAB đều

Suy ra: MA = MB = AB = \(4\sqrt 3 \) (cm)

Xét tam giác BHM vuông tại H có:

\(MH = BM.\sin \widehat {MBH} = 4\sqrt 3 .\sin {60^0} = 6\)(cm)

Xét tam giác MBC vuông tại B ta có

\(\tan \widehat {BCM} = \frac{{MB}}{{BC}} = \frac{{\sqrt 3 }}{2}\)

Mà \(\widehat {BCM} = \widehat {HAK}\)

Nên

 \(\begin{array}{l}\tan \widehat {HAK} = \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow \frac{{HK}}{{AH}} = \frac{{\sqrt 3 }}{2}\\ \Rightarrow HK = 3(cm)\end{array}\)

Ta có: MK = HM – HK = 6 – 3 = 3 (cm)

Vậy MK = 3 cm