Cho đường tròn tâm O và một điểm M nằm ngoài đường tròn đó. Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm). Vẽ đường kính BC của đường tròn (O). Gọi H là giao điểm của MO và AB, I là giao điểm thứ hai của đường thẳng MC với đường tròn (O), AI kéo dài cắt MO tại K.
a) Chứng minh tứ giác MAOB là một tứ giác nội tiếp.
b) Chứng minh AK vuông góc với IH
c) Cho biết BC = 2 cm, AC = 8 cm. Tính độ dài đoạn thẳng MK.
Cho đường tròn tâm O và một điểm M nằm ngoài đường tròn đó. Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm). Vẽ đường kính BC của đường tròn (O). Gọi H là giao điểm của MO và AB, I là giao điểm thứ hai của đường thẳng MC với đường tròn (O), AI kéo dài cắt MO tại K.
a) Chứng minh tứ giác MAOB là một tứ giác nội tiếp.
b) Chứng minh AK vuông góc với IH
c) Cho biết BC = 2 cm, AC = 8 cm. Tính độ dài đoạn thẳng MK.
Quảng cáo
Trả lời:
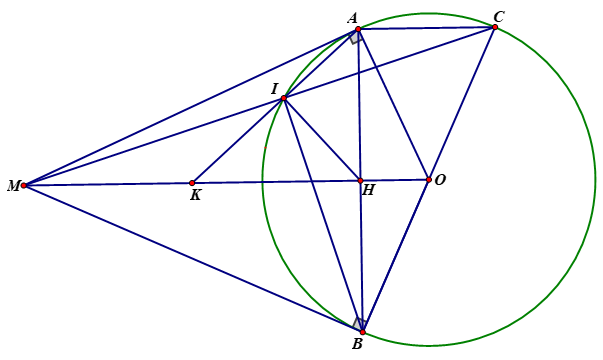
a) Xét tứ giác MAOB có
\(\widehat {MAO} + \widehat {MBO} = {90^0} + {90^0} = {180^0}\)
Nên tứ giác MAOB nội tiếp đường tròn đường kính MO
b) Xét (O) có MA, MB là 2 tiếp tuyến cắt nhau tại M
Nên MA = MB
Lại có : OA = OB (= R)
Do đó: MO là đường trung trực của AB
Suy ra: \({\rm{MO }} \bot {\rm{ AB}}\)
Xét \({\rm{\Delta MAI}}\)và \({\rm{\Delta MCA}}\)có:
\(\widehat {{\rm{AMI}}}\)chung
\(\widehat {{\rm{MAI}}}{\rm{ = }}\widehat {{\rm{ACM}}}\)(góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AI)
Do đó: \({\rm{\Delta MAI }} \sim {\rm{ }}\Delta {\rm{MCA}}\)
\(\begin{array}{l} \Rightarrow \frac{{MA}}{{MC}} = \frac{{MI}}{{MA}}\\ \Rightarrow M{A^2} = MI.MC\left( 1 \right)\end{array}\)
Áp dụng hệ thức lượng vào tam giác MAO vuông tại A, đường cao AH ta có
\(M{A^2} = MH.MO\left( 2 \right)\)
Từ (1), (2) suy ra: \(MI.MC = MH.MO\)
Xét \({\rm{\Delta MHI}}\)và \({\rm{\Delta MCO}}\)có:
\(\widehat {{\rm{OMC}}}\)chung
\(\frac{{MI}}{{MH}} = \frac{{MO}}{{MC}}\)(vì MI.MC = MH.MO)
Do đó: \({\rm{\Delta MHI }} \sim {\rm{ }}\Delta {\rm{MCO}}\)
\( \Rightarrow \widehat {MHI} = \widehat {MCO}\)
Mà \(\widehat {MCO} = \widehat {IAH}\)(2 góc nội tiếp cùng chắn cung IB)
Nên \(\widehat {MHI} = \widehat {IAH}\)
Ta có: \(\widehat {IHM} + \widehat {IHA} = {90^0}\)
Mà \(\widehat {MHI} = \widehat {IAH}\)
Nên \(\widehat {IAH} + \widehat {IHA} = {90^0}\)
Do đó tam giác AIH vuông tại I
Vậy: \(AK \bot IH\)
c) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta có
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow AB = 4\sqrt 3 \left( {cm} \right)\end{array}\)
Xét \({\rm{\Delta ABC}}\)vuông tại A, ta có
\(\begin{array}{l}\sin \widehat {ABC} = \frac{{AC}}{{BC}} = \frac{1}{2}\\ \Rightarrow \widehat {ABC} = {30^0}\end{array}\)
\( \Rightarrow \widehat {MBH} = {90^0} - {30^0} = {60^0}\)
Xét tam giác MAB cân tại M có
\(\widehat {MBH} = {60^0}\)
Nên tam giác MAB đều
Suy ra: MA = MB = AB = \(4\sqrt 3 \) (cm)
Xét tam giác BHM vuông tại H có:
\(MH = BM.\sin \widehat {MBH} = 4\sqrt 3 .\sin {60^0} = 6\)(cm)
Xét tam giác MBC vuông tại B ta có
\(\tan \widehat {BCM} = \frac{{MB}}{{BC}} = \frac{{\sqrt 3 }}{2}\)
Mà \(\widehat {BCM} = \widehat {HAK}\)
Nên
\(\begin{array}{l}\tan \widehat {HAK} = \frac{{\sqrt 3 }}{2}\\ \Leftrightarrow \frac{{HK}}{{AH}} = \frac{{\sqrt 3 }}{2}\\ \Rightarrow HK = 3(cm)\end{array}\)
Ta có: MK = HM – HK = 6 – 3 = 3 (cm)
Vậy MK = 3 cm
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số học sinh nam tham gia trồng cây là x (học sinh) \(x \in {N^*}\)x < 15
Vì nhóm gồm 15 học sinh (cả nam và nữ) tham gia buổi lao động trồng cây nên số học sinh nữ là 15 – x (học sinh)
Mỗi bạn nam trồng cây như nhau, số cây mỗi bạn nam trồng là \(\frac{{{\rm{54}}}}{{\rm{x}}}\) (cây)
Mỗi bạn nữ trồng cây như nhau, số cây mỗi bạn nam trồng là \(\frac{{30}}{{{\rm{15 - x}}}}\) (cây)
Vì mỗi bạn nam trồng được nhiều hơn mỗi bạn nữ 1 cây nên ta có phương trình:
\(\frac{{{\rm{54}}}}{{\rm{x}}}{\rm{ - }}\frac{{{\rm{30}}}}{{{\rm{15 - x}}}}{\rm{ = 1}}\)
\(\begin{array}{l} \Rightarrow {\rm{ 54}}\left( {{\rm{15 - x}}} \right){\rm{ - 30x = x}}\left( {{\rm{15 - x}}} \right)\\ \Leftrightarrow {\rm{ }}{{\rm{x}}^{\rm{2}}}{\rm{ - 99x + 810 = 0}}\\ \Leftrightarrow \left[ \begin{array}{l}{\rm{x = 90}}\\{\rm{x = 9}}\end{array} \right.\end{array}\)
So với điều kiện ta được x = 9
Vậy nhóm tham gia trồng cây có 9 học sinh nam và 15 – 9 = 6 học sinh nữ.
Lời giải
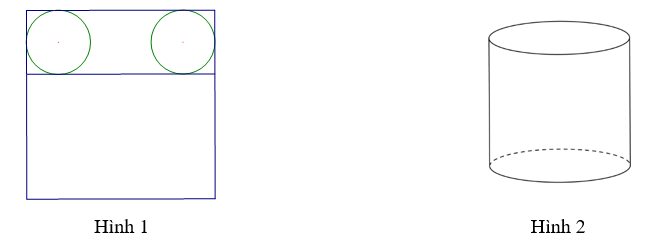
Gọi bán kính đường tròn là r (cm)
Vì chiều cao hình hộp nhỏ hơn 50 cm
Nên chu vi hình tròn bằng chiều dài hình chữ nhật bằng 50 cm
Do đó: \(2\pi r = 50 \Rightarrow r = \frac{{25}}{\pi }\)
Chiều cao của hình trụ là
\(50 - 2r = 50 - \frac{{50}}{\pi } \approx 34,085\)
Vậy chiều cao của cái hộp hình trụ gần bằng 34,085 cm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.