(1,5 điểm)
1) Cho biểu thức\(A = \frac{{\sqrt x + 4}}{{\sqrt x + 2}}\). Tính giá trị của biểu thức\(A\)với \(x = 36\).
2) Rút gọn biểu thức\(B = \left( {\frac{{\sqrt x }}{{\sqrt x + 4}} + \frac{4}{{\sqrt x - 4}}} \right) & :\frac{{x + 16}}{{\sqrt x + 2}}\) (với \(x \ge 0\), \(x \ne 16\)).
3) Với các biểu thức\(A\)và\(B\) , hãy tìm các giá trị nguyên của \(x\) để giá trị của biểu thức \(B\left( {A - 1} \right)\) là nhận giá trị nguyên.
(1,5 điểm)
1) Cho biểu thức\(A = \frac{{\sqrt x + 4}}{{\sqrt x + 2}}\). Tính giá trị của biểu thức\(A\)với \(x = 36\).
2) Rút gọn biểu thức\(B = \left( {\frac{{\sqrt x }}{{\sqrt x + 4}} + \frac{4}{{\sqrt x - 4}}} \right) & :\frac{{x + 16}}{{\sqrt x + 2}}\) (với \(x \ge 0\), \(x \ne 16\)).
3) Với các biểu thức\(A\)và\(B\) , hãy tìm các giá trị nguyên của \(x\) để giá trị của biểu thức \(B\left( {A - 1} \right)\) là nhận giá trị nguyên.Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 42 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1) Với \(x = 36\), ta có \(A = \frac{{\sqrt {36} + 4}}{{\sqrt {36} + 2}}\)\( = \frac{{10}}{8}\)\( = \frac{5}{4}\).
2) Với \(x \ge 0\), \(x \ne 16\) ta có
\(B = \left( {\frac{{\sqrt x \left( {\sqrt x - 4} \right)}}{{x - 16}} + \frac{{4\left( {\sqrt x + 4} \right)}}{{x - 16}}} \right).\frac{{\sqrt x + 2}}{{x + 16}} = \frac{{\left( {x + 16} \right)\left( {\sqrt x + 2} \right)}}{{\left( {x - 16} \right)\left( {x + 16} \right)}} = \frac{{\sqrt x + 2}}{{x - 16}}\).
3) Biểu thức \(B\left( {A - 1} \right) = \frac{{\sqrt x + 2}}{{x - 16}}.\left( {\frac{{\sqrt x + 4 - \sqrt x - 2}}{{\sqrt x + 2}}} \right) = \frac{2}{{x - 16}}\).
Ta có \(B\left( {A - 1} \right)\) nhận giá trị nguyên khi \(\frac{2}{{x - 16}}\) có giá trị nguyên.
Suy ra \(x - 16 \in \)Ư(2) = \(\left\{ { - 2;\, - 1;\,1;\,2} \right\}\). Suy ra \(x \in \left\{ {14;\,15;\,17;\,18} \right\}\)
Kết hợp điều kiện, để \(B\left( {A - 1} \right)\) nhận giá trị nguyên thì \(x \in \left\{ {14;\,15;\,17;\,18} \right\}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
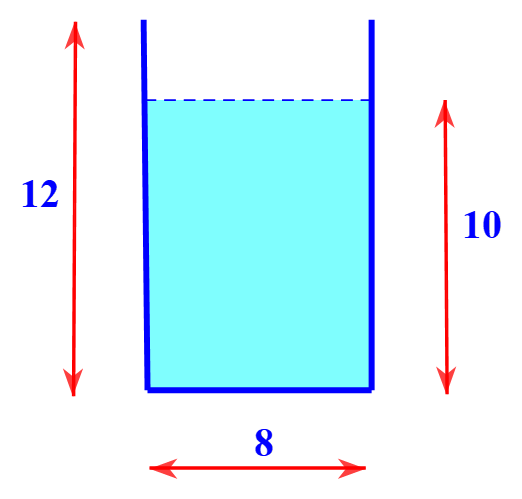
* Bán kính đáy của cốc nước hình trụ là:
\(R = 8:2 = 4(cm)\)
* Vì thể tích mực nước dâng lên bằng thể tích của viên bi nên:
\[{V_{nuoc\,dang}} = \pi {R^2}.{h_1} = 4\pi \]
\[{h_1} = \frac{{4\pi }}{{\pi {R^2}}} = \frac{4}{{16}} = 0,25(cm)\]
* Mực nước trong cốc sau khi thả viên bi là:
\[10{\rm{ }} + {\rm{ }}0,25{\rm{ }} = {\rm{ }}10,25{\rm{ }}\left( {cm} \right)\]
* Vậy mực nước trong cốc lúc này là\[{\rm{ }}10,25{\rm{ cm}}{\rm{.}}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
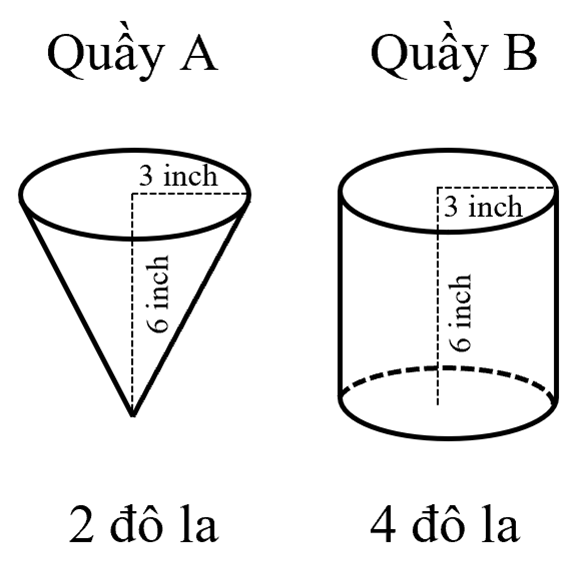
Thể tích hộp đựng hạt bắp rang bơ ở hình quầy A : \[V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.3^2}.6 = 18\pi \;(inc{h^3})\]
Thể tích hộp đựng hạt bắp rang bơ ở hình quầy B: \[V = \pi {R^2}h = \pi {.3^2}.6 = 54\pi \;(inc{h^3})\]
Thể tích hộp bắp rang bơ ở quầy B gấp thể tích hộp bắp rang bơ ở quầy A là \[54\pi :18\pi = \;3\](lần)
Mà giá tiền của quầy B gấp giá tiền của quầy A là \[4:2 = \;2\](lần)
Vậy Bạn H nên mua ở quầy B sẽ được lợi hơn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập