(4,0 điểm)
Một cốc nước có dạng hình trụ với đường kính đáy bằng 8 cm, chiều cao 12 cm và chứa một lượng nước cao 10 cm. Người ta thả từ từ một viên bi làm bằng thép đặc (không thấm nước) có thể tích là \[V{\rm{ }} = {\rm{ }}4\pi \left( {c{m^3}} \right)\] vào trong cốc. Hỏi mực nước trong cốc lúc này cao bao nhiêu cm?
(Giả sử độ dày của cốc không đáng kể).

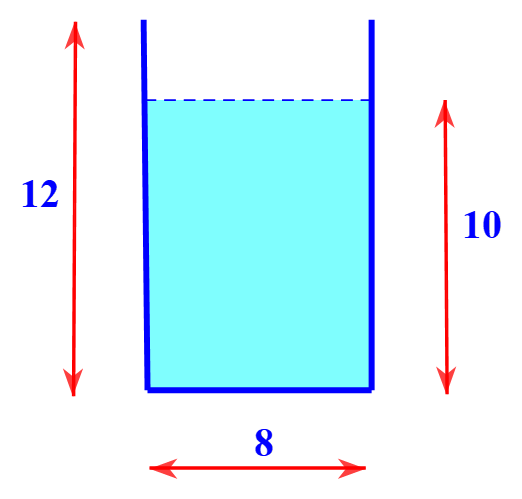
Một cốc nước có dạng hình trụ với đường kính đáy bằng 8 cm, chiều cao 12 cm và chứa một lượng nước cao 10 cm. Người ta thả từ từ một viên bi làm bằng thép đặc (không thấm nước) có thể tích là \[V{\rm{ }} = {\rm{ }}4\pi \left( {c{m^3}} \right)\] vào trong cốc. Hỏi mực nước trong cốc lúc này cao bao nhiêu cm?
(Giả sử độ dày của cốc không đáng kể).


Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 42 !!
Quảng cáo
Trả lời:
* Bán kính đáy của cốc nước hình trụ là:
\(R = 8:2 = 4(cm)\)
* Vì thể tích mực nước dâng lên bằng thể tích của viên bi nên:
\[{V_{nuoc\,dang}} = \pi {R^2}.{h_1} = 4\pi \]
\[{h_1} = \frac{{4\pi }}{{\pi {R^2}}} = \frac{4}{{16}} = 0,25(cm)\]
* Mực nước trong cốc sau khi thả viên bi là:
\[10{\rm{ }} + {\rm{ }}0,25{\rm{ }} = {\rm{ }}10,25{\rm{ }}\left( {cm} \right)\]
* Vậy mực nước trong cốc lúc này là\[{\rm{ }}10,25{\rm{ cm}}{\rm{.}}\]Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn tâm \((O)\), đường kính \(AB = 2R\). Trên đường tròn \((O)\), lấy điểm \(C\) bất kì (\(C\) không trùng với \(A\) và \(B\)). Tiếp tuyến của đường tròn \((O)\) tại \(A\) cắt tia \(BC\) ở điểm \(D.\) Gọi \(H\) là hình chiếu của \(A\) trên đường thẳng \(DO.\) Tia \(AH\) cắt đường tròn \((O)\)tại điểm \(F\) (không trùng với \(A\)).
a) Chứng minh tứ giác \(AHCD\) nội tiếp được một đường tròn.
b) Chứng minh \[\Delta CFH\] là tam giác vuông.
c) Tính giá trị của biểu thức \(S = \frac{{BH.BC}}{{BF}}\).
Cho đường tròn tâm \((O)\), đường kính \(AB = 2R\). Trên đường tròn \((O)\), lấy điểm \(C\) bất kì (\(C\) không trùng với \(A\) và \(B\)). Tiếp tuyến của đường tròn \((O)\) tại \(A\) cắt tia \(BC\) ở điểm \(D.\) Gọi \(H\) là hình chiếu của \(A\) trên đường thẳng \(DO.\) Tia \(AH\) cắt đường tròn \((O)\)tại điểm \(F\) (không trùng với \(A\)).
a) Chứng minh tứ giác \(AHCD\) nội tiếp được một đường tròn.
b) Chứng minh \[\Delta CFH\] là tam giác vuông.
c) Tính giá trị của biểu thức \(S = \frac{{BH.BC}}{{BF}}\).
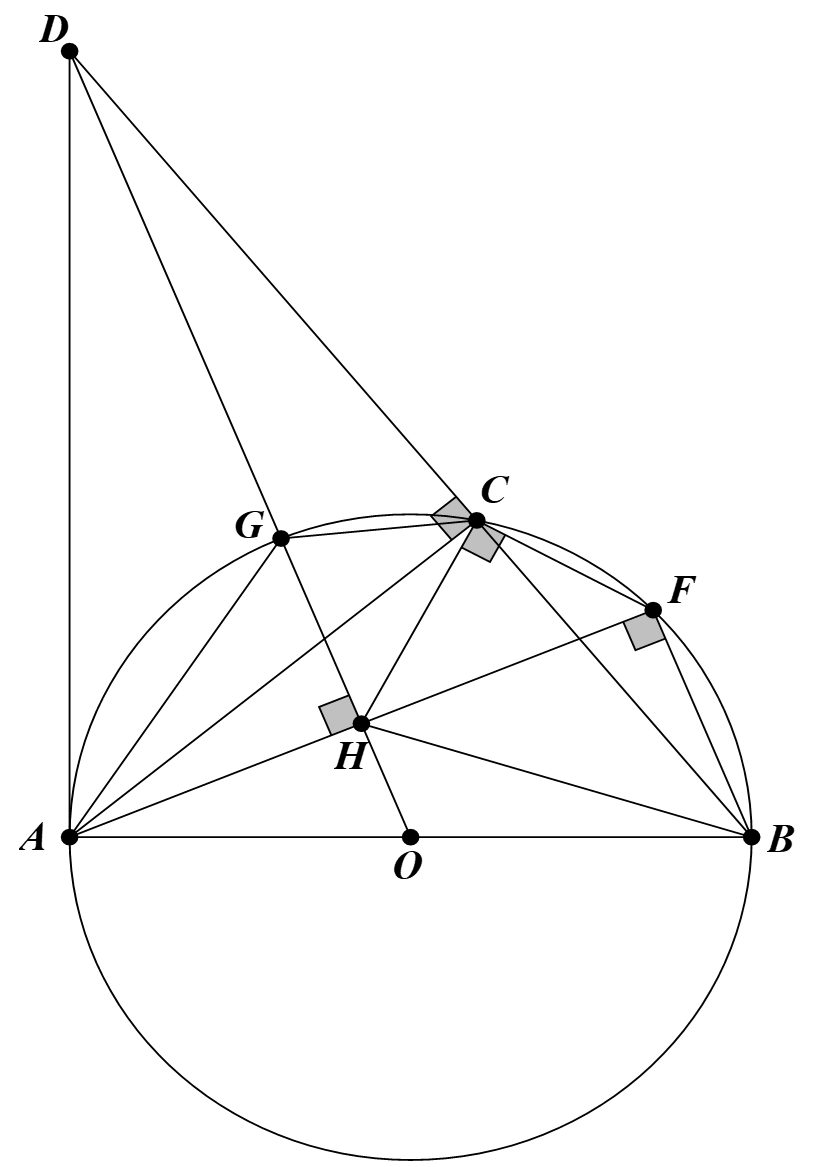
a) Do \(AH \bot DH\) \[ \Rightarrow \widehat {AHD} = 90^\circ \] nên A, H, D thuộc đường tròn đường kính AD (1)
Lại có \(\widehat {ACB} = {90^0}\)(góc nội tiếp chắn nửa đưởng tròn).
Suy ra \(\widehat {ACD} = {90^0}\) nên A, C, D thuộc đường tròn đường kính AD (1)
Từ (1) và (2) \( \Rightarrow \) A, H, C, D thuộc đường tròn đường kính AD hay tứ giác AHCD nội tiếp được một đường tròn.
b) Tứ giác AHCD nội tiếp \( \Rightarrow \widehat {HCB} = \widehat {DAH}\)
Ta có \(\widehat {BCF};\widehat {BAF}\) nội tiếp (O) cùng chắn \( \Rightarrow \widehat {BCF} = \widehat {BAF}\)
\( \Rightarrow \widehat {HCF} = \widehat {HCB} + \widehat {BCF} = \widehat {DAH} + \widehat {BAF} = \widehat {DAB} = 90^\circ .\)
Vậy \[\Delta CFH\] là tam giác vuông tại C.
c) Ta có: \[\widehat {FCB} = \widehat {HAB}\] (3) (hai góc nội tiếp cùng chắn cung ).
Tam giác OAD vuông tại A. Khi đó \[O{A^2} = OH.OD\]
Mà OA = OB nên \[O{B^2} = OH.OD \Rightarrow \frac{{OH}}{{OB}} = \frac{{OB}}{{OD}}\]
Suy ra hai tam giác OHB và OBD đồng dạng.
Suy ra \[\widehat {OBH} = \widehat {ODB}\] (4)
Ta lại có tứ giác AHCD nội tiếp nên \[\widehat {ODB} = \widehat {CAH}\] (5)
Tứ giác ABFC nội tiếp nên \[\widehat {CAH} = \widehat {CBF}\] (6)
Từ (4), (5) và (6) suy ra \[\widehat {OBH} = \widehat {CBF}\] (7)
Từ (3) và (7) suy ra hai tam giác HAB và FCB đồng dạng
Khi đó, ta có: \[\frac{{BC}}{{BA}} = \frac{{BF}}{{BH}} \Rightarrow \frac{{BC.BH}}{{BF}} = BA \Rightarrow \frac{{BC.BH}}{{BF}} = 2R\].
Vậy \[S = \frac{{BC.BH}}{{BF}} = 2R\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
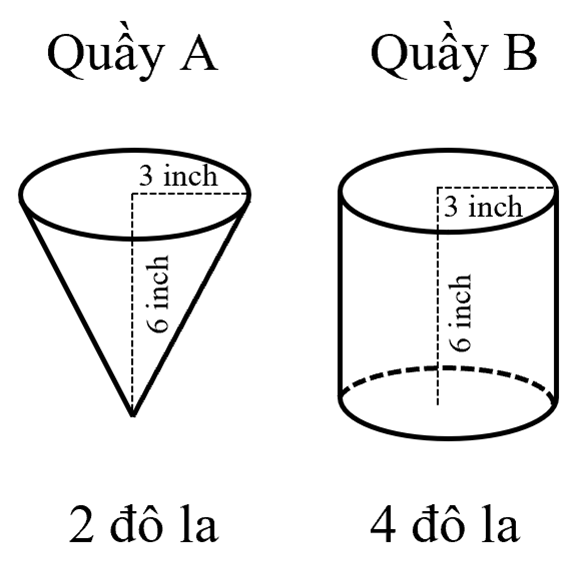
Thể tích hộp đựng hạt bắp rang bơ ở hình quầy A : \[V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.3^2}.6 = 18\pi \;(inc{h^3})\]
Thể tích hộp đựng hạt bắp rang bơ ở hình quầy B: \[V = \pi {R^2}h = \pi {.3^2}.6 = 54\pi \;(inc{h^3})\]
Thể tích hộp bắp rang bơ ở quầy B gấp thể tích hộp bắp rang bơ ở quầy A là \[54\pi :18\pi = \;3\](lần)
Mà giá tiền của quầy B gấp giá tiền của quầy A là \[4:2 = \;2\](lần)
Vậy Bạn H nên mua ở quầy B sẽ được lợi hơn.
Lời giải
Gọi \[x\] (quyển) là số vở mà Thanh có thể mua. Theo bài ta có bất phương trình
\[\begin{array}{l}17x + 18 \le 100\\\,\,\,\,\,\,\,\,\,\,17x \le 100 - 18\\\,\,\,\,\,\,\,\,\,\,\,\,17\,x \le 82\\\,\,\,\,\,\,\,\,\,\,\,\,\,x \le \frac{{82}}{{17}}\end{array}\]
Vì số vở là số tự nhiên nên Thanh có thể mua nhiều nhất \[4\] quyển vở
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.