Cho hàm số \(y = f\left( x \right) = - {x^3} + 12x\) và gọi \(F\left( x \right)\) là một nguyên hàm của hàm số \(y = f\left( x \right)\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 0 \right) = 2\).

Đáp án: 7900.

\[C(x) = \int {C'(x)d{\rm{x}} = } \int {(3{{\rm{x}}^2} - 4x + 10} )d{\rm{x}} = {{\rm{x}}^3} - 2{x^2} + 10x + C\]

Ta có \[C(0) = 500 \Rightarrow C = 500 \Rightarrow C(x) = {x^3} - 2{{\rm{x}}^2} + 10{\rm{x}} + 500\]

\[L(x) = 270{\rm{x}} - ({x^3} - 2{{\rm{x}}^2} + 10{\rm{x}} + 500) =  - {x^3} + 2{x^2} + 260{\rm{x}} - 500 \Rightarrow L'(x) =  - 3{{\rm{x}}^2} + 4{\rm{x}} + 260\].

\[L'(x) = 0 \Leftrightarrow x = 10;x =  - \frac{{26}}{3}\]

Vì \[0 \le x \le 20\] nên có \[L(0) = 500;L(10) = 1400;L(20) = 7900\].

Vậy lợi nhuận tối đa là 7900 nghìn đồng.

Đáp án: 0,92.

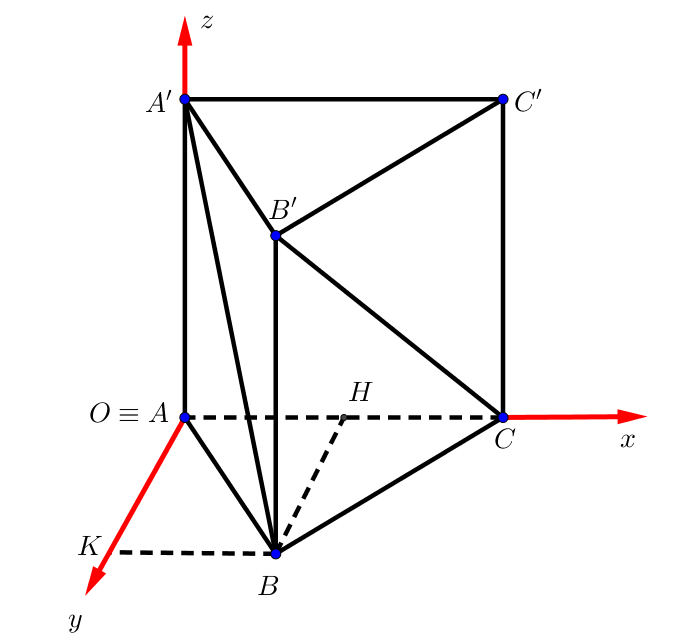
Chọn hệ trục tọa độ \(Oxyz\) như hình vẽ.

Ta tìm được \(A'\left( {0;0;\sqrt 2 } \right)\), \(C\left( {1;0;0} \right)\).

\({x_B} = AH = \frac{1}{2}AC = \frac{1}{2}\).

\({y_B} = BH = \frac{{AC\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{2}\).

Suy ra \(B\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\).

Do đó \(B'\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};1} \right)\) (Do \(B\) là hình chiếu của \(B'\) lên \(\left( {Oxy} \right)\)).

\(A'B\) đi qua điểm \(B\left( {\frac{1}{2};\frac{{\sqrt 3 }}{2};0} \right)\) và có 1 vectơ chỉ phương là \(\overrightarrow {A'B}  = \left( {\frac{1}{2};\frac{{\sqrt 3 }}{2}; - \sqrt 2 } \right)\).

\(B'C\) đi qua điểm \(C\left( {1;0;0} \right)\) và có 1 vectơ chỉ phương là \(\overrightarrow {B'C}  = \left( {\frac{1}{2}; - \frac{{\sqrt 3 }}{2}; - 1} \right)\).

\(d\left( {A'B,B'C} \right) = \frac{{\left| {\left[ {\overrightarrow {A'B} ,\overrightarrow {B'C} } \right] \cdot \overrightarrow {BC} } \right|}}{{\left| {\left[ {\overrightarrow {A'B} ,\overrightarrow {B'C} } \right]} \right|}} \approx 0,92\).