Diện tích bao phủ của cỏ Posidonia (một loài tảo biển) trên đáy ở một vùng vịnh theo thời gian được một nhóm các nhà sinh vật học quan sát và mô hình hoá bởi hàm số \(f\left( t \right) = \frac{k}{{1 + 14{e^{ - 0,3t}}}}\) (hecta), trong đó thời gian \(t\) tính bằng năm, \(k\) là số thực dương. Năm 2024 (ứng với \(t = 0\)) là thời điểm các nhà sinh vật học bắt đầu quan sát, lúc đó diện tích của cỏ Posidonia đã bao phủ là 1 (hecta).

Đáp án: 23.4.

Hàm lợi nhuận là:

\(L\left( x \right) = 21Q\left( x \right) - 13Q\left( x \right) - x\)\( = 8Q\left( x \right) - x\)\( = 10000 + 2028\ln \left( {3 + x} \right) - x\) (triệu đồng)

\(L'\left( x \right) = \frac{{2028}}{{3 + x}} - 1 = \frac{{2025 - x}}{{3 + x}}\);

\(L'\left( x \right) = 0 \Leftrightarrow x = 2025\)

\(L''\left( x \right) =  - \frac{{2028}}{{{{\left( {3 + x} \right)}^2}}}\); \(L''\left( {2025} \right) < 0\) nên hàm số đạt cực đại tại \(x = 2025\)

\({L_{\max }} = L\left( {2025} \right) = 23417,825\) (triệu đồng) \( \Rightarrow p = 23,4\) (tỷ đồng)

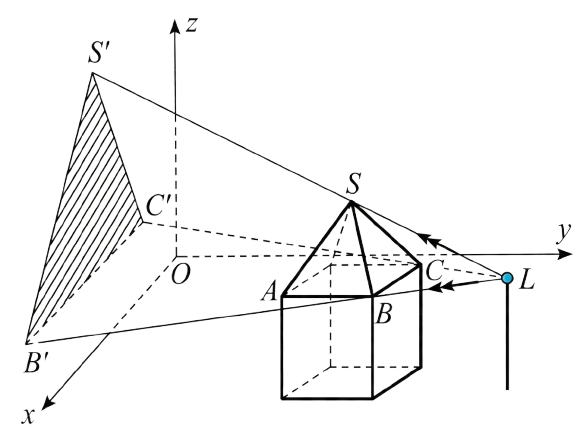
Chọn a) Đúng | b) Sai | c) Đúng | d) Đúng.

a) Vì \({z_A} = {z_B} = {z_C} = {z_D} = 2\)nên đáy của mái nhà nằm trên mặt phẳng \(z - 2 = 0\).

b) Tọa độ đinh chóp của mái nhà là \(S(5;4;5)\).

Gọi I là tâm của ABCD. Có I là trung điểm của AC nên \[I\left( {5;5;2} \right)\]. Có \(SI \bot \left( {ABCD} \right)\) nên \(S\left( {5;5;z} \right)\) với z > 2. Vì \(SI = 2 \Rightarrow \sqrt[{}]{{{0^2} + {0^2} + {{\left( {z - 2} \right)}^2}}} = 2 \Rightarrow \left| {z - 2} \right| = 2\) và \({z_S} > 2 \Rightarrow S\left( {5;5;4} \right)\)

c) Có \(\overrightarrow {SB}  = \left( {1;1; - 2} \right)\) và \(\overrightarrow {SC}  = \left( { - 1;1; - 2} \right)\). Do đó mặt phẳng (SBC) có 1 vectơ pháp tuyến là \(\left[ {\overrightarrow {SB} ;\overrightarrow {SC} } \right] = \left( {0;4;2} \right)\). Mặt phẳng (Oxz) có 1 vectơ pháp tuyến là \(\overrightarrow k  = \left( {0;1;0} \right)\)

Do đó góc giữa hai mặt phẳng \((SBC)\) và \((Oxz)\) là \(\varphi \) thì \[\cos \varphi  = \frac{{\left| {0 + 4 + 0} \right|}}{{\sqrt[{}]{{{0^2} + {4^2} + {2^2}}}.\sqrt[{}]{{{0^2} + {1^2} + {0^2}}}}} = \frac{2}{{\sqrt 5 }}\].

d) Phương trình tham số của đường thẳng \(LB\) là: \(\left\{ \begin{array}{l}x = 5 + t\\y = 10 - 4t\\z = 2\end{array} \right.\)

\(B'\left( {5 + t;\,10 - 5t;\,2} \right)\) là giao điểm của \(LB\) và mặt phẳng \(\left( {Oxz} \right)\): \(y = 0\).

Suy ra: \(10 - 4t = 0\, \Leftrightarrow \,t = 2,5\). Do đó \(B'\left( {7,5;\,0;\,2} \right)\).

Phương trình tham số của đường thẳng \(LC\) là: \(\left\{ \begin{array}{l}x = 5 - t\\y = 10 - 4t\\z = 2\end{array} \right.\)

\(C'\left( {5 - t;\,10 - 4t;\,2} \right)\) là giao điểm của \(LC\) và mặt phẳng \(\left( {Oxz} \right)\): \(y = 0\).

Suy ra: \(10 - 4t = 0\, \Leftrightarrow \,t = \frac{5}{2}\). Do đó \(C'\left( {\frac{5}{2};\,0;\,2} \right)\).

Phương trình tham số của đường thẳng \(LS\) là: \(\left\{ \begin{array}{l}x = 5\\y = 10 - 5t\\z = 2 + 2t\end{array} \right.\)

Ta có \(S'\left( {5;\,10 - 5t;\,2} \right)\) là giao điểm của \(LS\) và mặt phẳng \(\left( {Oxz} \right)\): \(y = 0\).

Suy ra: \(10 - 5t = 0\, \Leftrightarrow \,t = 2\). Do đó \(S'\left( {5;\,0;\,6} \right)\).

Ta có: \(S'B' = \frac{{\sqrt {89} }}{2}\), \(S'C' = \frac{{\sqrt {89} }}{2};\,B'C' = 5\)

Áp dụng công thức hê-rông tao có: \({S_{\Delta S'B'C'}} = \sqrt {\frac{{5 + \sqrt {89} }}{2}.\frac{5}{2}.\frac{5}{2}.\left( {\frac{{\sqrt {89}  - 5}}{2}} \right)}  = 10\)