Có 25 chai rượu Vang Opus One đang đựng trong thùng \(A\) và thùng \(B\), trong mỗi thùng đều có chai Vang thật và Vang giả ( các chai Vang đều giống nhau về mẫu mã, chai Vang giả được chủ quán Bar đánh dấu để phân biệt) và số chai rượu ở thùng \(A\) nhiều hơn ở thùng \(B\). Biết khi lấy ngẫu nhiên ở mỗi thùng một chai Vang thì xác suất lấy được hai chai Vang thật là \(\frac{{65}}{{144}}\). Nhân viên quầy bar có \(P\) cách để xếp hết 25 chai Vang này lên kệ rượu thành một hàng ngang sao cho không có hai chai Vang giả nào được xếp kề nhau. Tính giá trị của \(\frac{P}{{12}}\).

Đáp án: 23.4.

Hàm lợi nhuận là:

\(L\left( x \right) = 21Q\left( x \right) - 13Q\left( x \right) - x\)\( = 8Q\left( x \right) - x\)\( = 10000 + 2028\ln \left( {3 + x} \right) - x\) (triệu đồng)

\(L'\left( x \right) = \frac{{2028}}{{3 + x}} - 1 = \frac{{2025 - x}}{{3 + x}}\);

\(L'\left( x \right) = 0 \Leftrightarrow x = 2025\)

\(L''\left( x \right) =  - \frac{{2028}}{{{{\left( {3 + x} \right)}^2}}}\); \(L''\left( {2025} \right) < 0\) nên hàm số đạt cực đại tại \(x = 2025\)

\({L_{\max }} = L\left( {2025} \right) = 23417,825\) (triệu đồng) \( \Rightarrow p = 23,4\) (tỷ đồng)

Chọn a) Đúng | b) Sai | c) Đúng | d) Đúng.

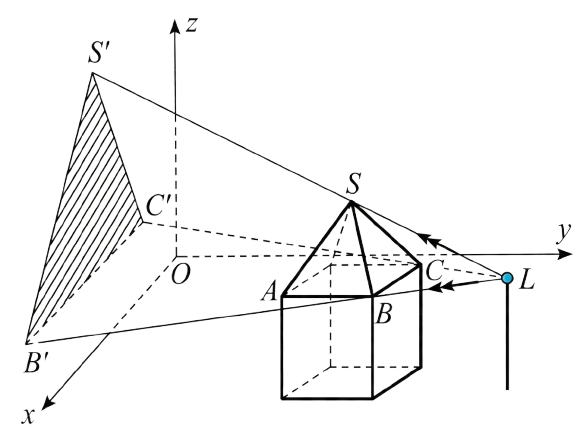
a) Vì \({z_A} = {z_B} = {z_C} = {z_D} = 2\)nên đáy của mái nhà nằm trên mặt phẳng \(z - 2 = 0\).

b) Tọa độ đinh chóp của mái nhà là \(S(5;4;5)\).

Gọi I là tâm của ABCD. Có I là trung điểm của AC nên \[I\left( {5;5;2} \right)\]. Có \(SI \bot \left( {ABCD} \right)\) nên \(S\left( {5;5;z} \right)\) với z > 2. Vì \(SI = 2 \Rightarrow \sqrt[{}]{{{0^2} + {0^2} + {{\left( {z - 2} \right)}^2}}} = 2 \Rightarrow \left| {z - 2} \right| = 2\) và \({z_S} > 2 \Rightarrow S\left( {5;5;4} \right)\)

c) Có \(\overrightarrow {SB}  = \left( {1;1; - 2} \right)\) và \(\overrightarrow {SC}  = \left( { - 1;1; - 2} \right)\). Do đó mặt phẳng (SBC) có 1 vectơ pháp tuyến là \(\left[ {\overrightarrow {SB} ;\overrightarrow {SC} } \right] = \left( {0;4;2} \right)\). Mặt phẳng (Oxz) có 1 vectơ pháp tuyến là \(\overrightarrow k  = \left( {0;1;0} \right)\)

Do đó góc giữa hai mặt phẳng \((SBC)\) và \((Oxz)\) là \(\varphi \) thì \[\cos \varphi  = \frac{{\left| {0 + 4 + 0} \right|}}{{\sqrt[{}]{{{0^2} + {4^2} + {2^2}}}.\sqrt[{}]{{{0^2} + {1^2} + {0^2}}}}} = \frac{2}{{\sqrt 5 }}\].

d) Phương trình tham số của đường thẳng \(LB\) là: \(\left\{ \begin{array}{l}x = 5 + t\\y = 10 - 4t\\z = 2\end{array} \right.\)

\(B'\left( {5 + t;\,10 - 5t;\,2} \right)\) là giao điểm của \(LB\) và mặt phẳng \(\left( {Oxz} \right)\): \(y = 0\).

Suy ra: \(10 - 4t = 0\, \Leftrightarrow \,t = 2,5\). Do đó \(B'\left( {7,5;\,0;\,2} \right)\).

Phương trình tham số của đường thẳng \(LC\) là: \(\left\{ \begin{array}{l}x = 5 - t\\y = 10 - 4t\\z = 2\end{array} \right.\)

\(C'\left( {5 - t;\,10 - 4t;\,2} \right)\) là giao điểm của \(LC\) và mặt phẳng \(\left( {Oxz} \right)\): \(y = 0\).

Suy ra: \(10 - 4t = 0\, \Leftrightarrow \,t = \frac{5}{2}\). Do đó \(C'\left( {\frac{5}{2};\,0;\,2} \right)\).

Phương trình tham số của đường thẳng \(LS\) là: \(\left\{ \begin{array}{l}x = 5\\y = 10 - 5t\\z = 2 + 2t\end{array} \right.\)

Ta có \(S'\left( {5;\,10 - 5t;\,2} \right)\) là giao điểm của \(LS\) và mặt phẳng \(\left( {Oxz} \right)\): \(y = 0\).

Suy ra: \(10 - 5t = 0\, \Leftrightarrow \,t = 2\). Do đó \(S'\left( {5;\,0;\,6} \right)\).

Ta có: \(S'B' = \frac{{\sqrt {89} }}{2}\), \(S'C' = \frac{{\sqrt {89} }}{2};\,B'C' = 5\)

Áp dụng công thức hê-rông tao có: \({S_{\Delta S'B'C'}} = \sqrt {\frac{{5 + \sqrt {89} }}{2}.\frac{5}{2}.\frac{5}{2}.\left( {\frac{{\sqrt {89}  - 5}}{2}} \right)}  = 10\)