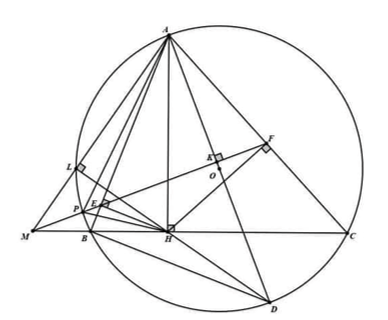
Cho tam giác \(ABC\) nhọn (\(AB < AC\)) có đường cao \(AH\) và nội tiếp đường tròn \(\left( O \right)\). Gọi \(E,F\) lần lượt là hình chiếu của \(H\) lên các cạnh \(AB,AC\). Đường kính \(AD\) của \(\left( O \right)\) cắt \(EF\) tại \(K\) và \(DH\) cắt \(\left( O \right)\) tại \(L\) (\(L\) khác \(D\)).
a) Chứng minh các tứ giác \(AEHF\) và \(ALHF\) nội tiếp.
b) Chứng minh tứ giác \(BEFC\) nội tiếp và \(AD\) vuông góc với \[EF\] tại \[K\].
c) Tia \[FE\] cắt \(\left( O \right)\) tại \(P\) và cắt \(BC\) tại \(M\). Chứng minh \(AP = AH\) và ba điểm \(A,L,M\) thẳng hàng.
Cho tam giác \(ABC\) nhọn (\(AB < AC\)) có đường cao \(AH\) và nội tiếp đường tròn \(\left( O \right)\). Gọi \(E,F\) lần lượt là hình chiếu của \(H\) lên các cạnh \(AB,AC\). Đường kính \(AD\) của \(\left( O \right)\) cắt \(EF\) tại \(K\) và \(DH\) cắt \(\left( O \right)\) tại \(L\) (\(L\) khác \(D\)).
a) Chứng minh các tứ giác \(AEHF\) và \(ALHF\) nội tiếp.
b) Chứng minh tứ giác \(BEFC\) nội tiếp và \(AD\) vuông góc với \[EF\] tại \[K\].
c) Tia \[FE\] cắt \(\left( O \right)\) tại \(P\) và cắt \(BC\) tại \(M\). Chứng minh \(AP = AH\) và ba điểm \(A,L,M\) thẳng hàng.
Quảng cáo
Trả lời:
a) Xét tứ giác \(AEHF\) có \(\widehat {AEF} = \widehat {AFH} = {90^ \circ }\) nên tứ giác này nội tiếp được.
Xét tứ giác \(ALHF\) có \(\widehat {ALH} = \widehat {ALD} = {90^ \circ }\) do chắn đường kính \(AD\).
Và \(\widehat {ALH} = \widehat {AFH} = {90^ \circ }\) nên tứ giác này nội tiếp được.
b) Ta có \(\Delta AHB\) vuông tại \(H\) nên \(AE.AB = A{H^2}\)(hệ thức lượng)
Ta lại có \(\Delta AHC\) vuông tại \(H\) nên \(AF.AC = A{H^2}\)(hệ thức lượng)
\( \Rightarrow AE.AB = AF.AC\) hay \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\)
\( \Rightarrow \Delta AEF \sim \Delta ACB\) (c.g.c)\( \Rightarrow \widehat {AEF} = \widehat {ACB}\)
Nên \(\widehat {ACB} + \widehat {FEB} = \widehat {AEF} + \widehat {FEB} = {180^ \circ }\). Mà 2 góc đối nhau nên tứ giác \(BCFE\) nội tiếp.
Xét \(\widehat {EAD} + \widehat {FEA} = \widehat {BAD} + \widehat {ACB} = \widehat {BAD} + \widehat {ADB} = {90^ \circ }\)\( \Rightarrow AD \bot EF\) tại \(K\).
c) \(\Delta APD\) vuông ở \(P\), có \(PK\) là đường cao \( \Rightarrow A{P^2} = AK.AD\).
Mà \(DKEB\) là tứ giác nội tiếp (do \(\widehat K + \widehat B = {90^ \circ }\)) \( \Rightarrow AK.AD = AE.AB\) (tính chất cát tuyến)
Mà \(\Delta ABH\) vuông tại \(H\) và có đường cao từ đỉnh vuông là \(AE\) suy ra \(AE.AB = A{H^2}\).
Từ trên suy ra \(A{P^2} = AK.AD = AE.AB = A{H^2}\)
Hay \(AP = AH\).
Giả sử \(MA\) cắt đường tròn tại \(L'\) khác \(A\). Khi đó \(ML'.MA = MB.MC\)
Ta có \(BCFE\) nội tiếp được nên \(MB.MC = ME.MF\)
Lại có \(ALEE\) nội tiếp được nên \(ME.MF = ML.MA\)
Từ trên suy ra \(ML'.MA = ML.MA\)\( \Rightarrow ML' = ML\) hay \(L' \equiv L\).
Vậy \(M,L,A\) thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Nếu mua nhiều hơn 10 bông hồng thì từ bông thứ 11 trở đi, mỗi bông được giảm \[10\% \] trên giá niêm yết. Nên giá một bông hồng sau khi giảm từ bông hồng thứ 11 là:
\[15000\left( {100\% - 10\% } \right) = 13500\](đồng)
Nếu mua nhiều hơn 20 bông hồng thì từ bông thứ 21 trở đi, mỗi bông được giảm \[20\% \] trên giá đã giảm. Nên giá một bông hồng sau khi giảm từ bông hồng thứ 21 là:
\[13500\left( {100\% - 20\% } \right) = 10800\](đồng)
Khách hàng mua 30 bông hồng tại cửa hàng \[A\] thì phải trả bao nhiêu tiền là:
\[10.15000 + 10.13500 + 10.10800 = 393000\](đồng).
Vậy khách hàng phải trả cho cửa hàng \[A\] số tiền là \[393000\](đồng).
b) Ta thấy số tiền Thảo đã trả lớn hơn số tiền mua 30 bông hồng nên gọi số bông hồng từ bông thứ 21 trở đi là \[x\] (\[x \in {\mathbb{N}^*},\]bông).
Ta có: \[10.15000 + 10.13500 + x.10800 = 555000 \Leftrightarrow x.10800 = 270000 \Leftrightarrow x = 25\]
Vậy số bông hồng bạn Thảo đã mua là: \[20 + 25 = 45\](bông).
Lời giải
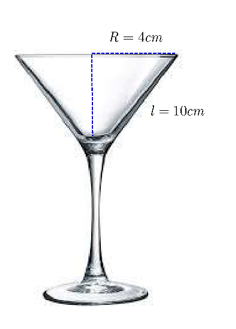
a) Chiều cao phần chứa nước của ly là: \(h = \sqrt {{l^2} - {R^2}} = 2\sqrt {21} \,(cm)\).
Thể tích phần chứa nước của ly là: \(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.4^2}.2\sqrt {21} \approx 154\,\,(c{m^3})\).
b) Lượng nước mỗi người uống là: \(3.90\% V = 415,8\,(c{m^3})\).
Đổi \(1,2\) lít \( = 1200\,c{m^3}\)
Ta thấy \(\frac{{14.415,8}}{{1200}} \approx 4,8\).
Vậy bạn Nam cần chuẩn bị ít nhất \(5\) hộp nước trái cây.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.