(2,5 điểm)

Cho tam giác nhọn \[ABC\left( {AB < AC} \right)\] nội tiếp đường tròn \[\left( O \right)\] và có các đường cao \[AD\,,\,\,BE\,,\,\,CF\] cắt nhau tại điểm \[H\].

a)  Chứng minh tứ giác \[BFEC\] nội tiếp

b) Vẽ đường kính \[AT\] của đường tròn \[\left( O \right)\]. Chứng minh \[\Delta ADB\] đồng dạng với \[\Delta ACT\] và \[2\widehat {HEF} + \widehat {AOC} = 180^\circ \].

c)  Vẽ \[CI\] vuông góc với \[AT\] tại \[I\]. Gọi \[M\] là trung điểm của \[BC\]. Chứng minh ba điểm \[F\,,\,\,M\,,\,\,I\] thẳng hàng.

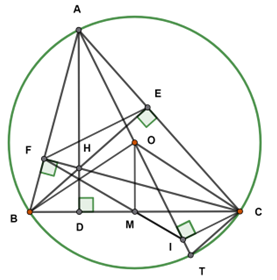
a)  Xét tứ giác \[BCEF\] ta có: \[\widehat {BFC} = \widehat {BEC} = 90^\circ \]\[(BE,CF\]là đường cao)

Suy ra tứ giác \[BCEF\]nội tiếp đường tròn đường kính \[BC\].

b) Ta có \[\widehat {ACT} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn \[(O)\]).

Xét \[\Delta ADB\] và \[\Delta ACT\] ta có:

\[\widehat {ACT} = \widehat {ADB} = 90^\circ \]

\[\widehat {ABD} = \widehat {ATC}\] (cùng chắn cung \[AC\])                   

Do đó  (g.g)                    

Ta có:  (cùng chắn cung \[AC\])

Vì tứ giác \[BCEF\] nội tiếp nên          

  \[ \Rightarrow \]

   \[ \Rightarrow \]                    

c)  Ta có \[\Delta AOC\]cân tại \[O\], \[OM\]là đường trung tuyến nên \[OM\] cũng là đường phân giác, đường cao

Do đó \[\widehat {BAC} = \widehat {MOC} = \frac{1}{2}\widehat {BOC}\]

Tương tự \[\widehat {BAC} + \widehat {ACF} = \widehat {MOC} + \widehat {OCM} = 90^\circ \]

Nên \[\widehat {ACF} = \widehat {OCM}\] (1)

Xét tứ giác \[OMIC\]ta có \[\widehat {OMC} = \widehat {OIC} = 90^\circ \]

Suy ta tứ giác \[OMIC\] nội tiếp đường tròn đường kính \[OC\]

Do đó \[\widehat {OCM} = \widehat {OIM}\] (cùng chắn cung \[OM\]) (2)

Xét tứ giác \[AFIC\] ta có\[\widehat {AFI} = \widehat {AIC} = 90^\circ \]

Suy ta tứ giác \[AFIC\] nội tiếp đường tròn đường kính \[AC\]

Do đó \[\widehat {AIF} = \widehat {ACF}\] (cùng chắn cung \[OM\]) (3)

Từ (1), (2) và (3) suy ra \[\widehat {AIF} = \widehat {OIM}\]

Do đó hai tia \[IF.\;IM\] trùng nhau.

Vậy ba điểm \[F\,,\,\,M\,,\,\,I\] thẳng hàng.