Cho hàm số \(y = f(x) = \frac{{a{x^2} + bx + c}}{{x + d}}\) có đồ thị là đường cong như hình vẽ dưới đây

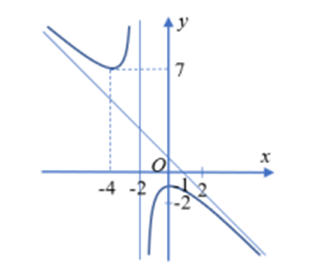
Biết đường tiệm cận xiên của đồ thị hàm số đi qua 2 điểm \(\left( {0;1} \right)\) và \(\left( {1;0} \right)\).

a- Sai; b – Sai; c – Đúng; d - Đúng

a) Trên khoảng \(\left( { - 4;0} \right)\) hàm số không liên tục nên hàm số không đồng biến trên khoảng \(\left( { - 4;0} \right)\). Vậy a - sai.

b) Tập xác định của hàm số \(D = \mathbb{R}\backslash \left\{ 2 \right\}\). Vậy b – Sai

c) Ta có đường tiệm cận xiên có phương trình: \({d_1}:y =  - x + 1\); đường tiệm cận đứng \({d_2}:x =  - 2\)

Vậy ta có \(y = f(x) =  - x + 1 + \frac{m}{{x + 2}}\)

Mà đồ thị hàm số đi qua điểm \(( - 4;7)\), nên \(m =  - 4\)

Vậy \(y = f(x) =  - x + 1 + \frac{{ - 4}}{{x + 2}} = \frac{{ - {x^2} - x - 2}}{{x + 2}}\). Khi đó \(a =  - 1;b =  - 1;c =  - 2;d = 2\)

Vậy \(a + b + c + d =  - 2\). Vậy c – đúng

d) Gọi \(M\left( {{x_o}; - {x_o} + 1 - \frac{4}{{{x_o} + 2}}} \right)\)

Tiếp tuyến với đồ thị hàm số tại điểm \(M\) có phương trình:

                                             \(y = \left( { - 1 + \frac{4}{{{{({x_o} + 2)}^2}}}} \right)\left( {x - {x_o}} \right) + \frac{{ - x_o^2 - {x_o} - 2}}{{{x_o} + 2}}\)     \(\left( \Delta  \right)\)

Gọi \(A\) là giao điểm của \({d_1} \cap \Delta \) , nên tọa độ điểm \(A\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}y = \left( { - 1 + \frac{4}{{{{({x_o} + 2)}^2}}}} \right)\left( {x - {x_o}} \right) + \frac{{ - x_o^2 - {x_o} - 2}}{{{x_o} + 2}}\\y =  - x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2{x_o} + 2\\y =  - 2{x_o} - 1\end{array} \right.\)\( \Rightarrow A\left( {2{x_o} + 2; - 2{x_o} - 1} \right)\)

Gọi \(B\) là giao điểm của \({d_2} \cap \Delta \) , nên tọa độ điểm \(B\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}y = \left( { - 1 + \frac{4}{{{{({x_o} + 2)}^2}}}} \right)\left( {x - {x_o}} \right) + \frac{{ - x_o^2 - {x_o} - 2}}{{{x_o} + 2}}\\x =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 2\\y = \frac{{3{x_o} - 2}}{{{x_o} + 2}}\end{array} \right.\)\( \Rightarrow B\left( { - 2;\frac{{3{x_o} - 2}}{{{x_o} + 2}}} \right)\)

Ta có \(MA = \sqrt {{{\left( {{x_o} + 2} \right)}^2} + {{\left( { - {x_o} - 2 + \frac{4}{{{x_o} + 2}}} \right)}^2}} \); 

\(MB = \sqrt {{{\left( { - {x_o} - 2} \right)}^2} + {{\left( {\frac{{ - x_o^2 - {x_o} - 2 - 3{x_o} + 2}}{{{x_o} + 2}}} \right)}^2}} \)\( = \sqrt {{{\left( { - {x_o} - 2} \right)}^2} + {{\left( { - {x_o} - 2 + \frac{4}{{{x_o} + 2}}} \right)}^2}} \)

\( = \sqrt {{{\left( {{x_o} + 2} \right)}^2} + {{\left( { - \left( {{x_o} + 2} \right) + \frac{4}{{{x_o} + 2}}} \right)}^2}} \)

Vậy \(MA.MB = {\left( { - {x_o} - 2} \right)^2} + {\left( { - {x_o} - 2 + \frac{4}{{{x_o} + 2}}} \right)^2}\), đặt \(t = {x_o} + 2\) ta có

\(MA.MB = {t^2} + {\left( {t - \frac{4}{t}} \right)^2} = 2{t^2} + \frac{{16}}{{{t^2}}} - 8 \ge 2\sqrt {2{t^2}.\frac{{16}}{{{t^2}}}}  - 8 = 8\sqrt 2  - 8\) (BDT cô si)

Khi đó \(MA.MB\) đạt giá trị nhỏ nhất là \(8\sqrt 2  - 8\). Vậy d – đúng.