Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm trường QV1-TT1-LVT lần 1 có đáp án
2339 người thi tuần này 4.6 2.9 K lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Thị Minh Khai (Hà Nội) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Liên trường THPT (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Đại học Vinh lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm liên trường Nghệ An có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Bắc Ninh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên ĐH KHTN Hà Nội lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Hưng Yên có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Gia Thiều (Hà Nội) có đáp án
Danh sách câu hỏi:
Câu 1
Lời giải
Chọn D
Hàm số \[y = {\left( {x - 3} \right)^2}{e^x}\] liên tục trên đoạn \[\left[ {0;2} \right]\].
Ta có \[y' = 2\left( {x - 3} \right){e^x} + {\left( {x - 3} \right)^2}{e^x} = {e^x}\left( {x - 3} \right)\left( {x - 1} \right)\].
Khi đó \[y' = 0 \Leftrightarrow {e^x}\left( {x - 3} \right)\left( {x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1{\rm{ }} \in \left[ {0;2} \right]\end{array} \right.\]
Do đó \[y\left( 0 \right) = 9\]; \[y\left( 1 \right) = 4e\]; \[y\left( 2 \right) = {e^2}\].
Vậy giá trị nhỏ nhất của hàm số \[y = {\left( {x - 3} \right)^2}{e^x}\] trên đoạn \[\left[ {0;2} \right]\] bằng \[y\left( 1 \right) = 4e\].
Câu 2
Lời giải
Chọn A
Điều kiện \[\left\{ \begin{array}{l}x - 2 > 0\\{x^2} - 3x + 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 2\\\left[ \begin{array}{l}x < 1\\x > 2\end{array} \right.\end{array} \right. \Leftrightarrow x > 2\].
Bất phương trình \[1 + {\log _2}\left( {x - 2} \right) > {\log _2}\left( {{x^2} - 3x + 2} \right)\]
\[ \Leftrightarrow {\log _2}2 + {\log _2}\left( {x - 2} \right) > {\log _2}\left( {{x^2} - 3x + 2} \right)\]
\[ \Leftrightarrow {\log _2}2\left( {x - 2} \right) > {\log _2}\left( {{x^2} - 3x + 2} \right)\]
\[ \Rightarrow 2\left( {x - 2} \right) > {x^2} - 3x + 2 \Leftrightarrow {x^2} - 5x + 6 < 0\]
\[ \Leftrightarrow 2 < x < 3\]
Kết hợp điều kiện \[2 < x < 3\]
Câu 3
A. Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \[\left( { - 2; + \infty } \right)\] .
B. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \[\left( { - \frac{1}{2};0} \right)\].
C. Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \[\left( { - \frac{5}{2}; - 2} \right)\].
Lời giải
Chọn D
Dựa vào đồ thị \[f'\left( x \right)\] cắt trục hoành tại \[x = - 3;x = - 2;x = 0\] (nghiệm kép)
Nên ta có bảng xét dấu như sau
![Cho hàm số \[y = f\left( x \right)\] xác định, có đạo hàm trên \[\mathbb{R}\] và \[f'\left( x \right)\] có đồ thị như hình vẽ Mệnh đề nào sau đây đúng? (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid1-1767808261.png)
Dựa vào bảng xét dấu hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \[\left( { - \infty ; - 3} \right)\].
Câu 4
Lời giải
Chọn D
Dựa vào bảng biến thiên, giá trị cực đại của hàm số \[y = f\left( x \right)\] là \[0\]
Câu 5
Lời giải
Chọn D
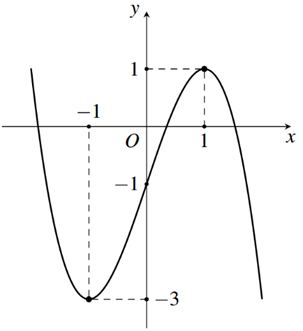
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\) (Loại A, B).
Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt (Loại C).
Vậy đường cong trong hình vẽ là đồ thị của hàm số \(y = - {x^3} + 3x - 1\).
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[x = \frac{{2\pi }}{3} + k2\pi ,x = \frac{\pi }{3} + k2\pi \].
B. \[x = \frac{\pi }{3} + k\pi ,x = - \frac{\pi }{3} + k\pi \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
a) Chi phí thấp nhất mà ông A trả cho công nhân làm bể nước theo yêu cầu là 3072000 đồng.
b) Chiều cao của bể nước là \(\frac{{384}}{{{x^2}}}\) (dm).
c) Diện tích xung quanh của bể chứa nước là \(\frac{{3072}}{x}\,\left( {{\rm{d}}{{\rm{m}}^2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
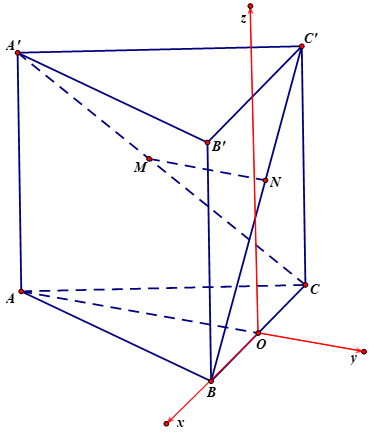
a) \(\overrightarrow {AB} .\overrightarrow {BC} = 0\).
b) Tọa độ vecto \(\overrightarrow {BC} \)là \[\left( { - 2\,;\,4\,;\,2} \right)\].
c) Điểm \(G\left( {\frac{7}{3}\,;\,\frac{9}{3}\,;\,0} \right)\)là trọng tâm tam giác \(ABC\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
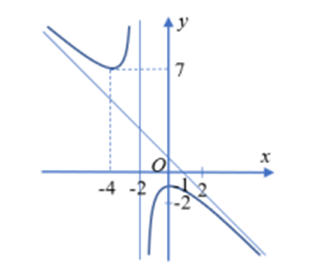
a) [TH] Hàm số đồng biến trên khoảng \(\left( { - 4;0} \right)\)
b) [NB] Tập xác định của hàm số là \(\mathbb{R}\backslash \left\{ 2 \right\}\)
c) [TH] Ta có \(a + b + c + d = - 2\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
a) [VD,VDC] Xác suất chọn được 6 viên bi đủ ba màu, đồng thời ba số \(x - y,y - z,z - x\) theo thứ tự lập thành cấp số cộng là \(\frac{{40}}{{221}}\).
b) [TH] Xác suất chọn được ít nhất một viên bi màu xanh nhỏ hơn \(0,95\).
c) [TH] Xác suất chọn được 6 viên bi toàn màu xanh là \(\frac{1}{{2652}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \[y = f\left( x \right)\] xác định, có đạo hàm trên \[\mathbb{R}\] và \[f'\left( x \right)\] có đồ thị như hình vẽ Mệnh đề nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid0-1767808254.png)
![Cho hàm số \[y = f\left( x \right)\] có bảng biến thiên sau: Giá trị cực đại của hàm số \[y = f\left( x \right)\] là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid2-1767808321.png)
![Một chiếc máy bay đang bay trong hệ trục toạ độ \[Oxyz\] với mặt phẳng \[(Oxy)\] là mặt đất như hình vẽ. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid7-1767809067.png)
![Từ một tấm bìa mỏng hình lục giác đều cạnh \[4\sqrt 3 \;dm\], bạn An cắt bỏ sáu tam giác cân bằng nhau có cạnh đáy là cạnh của hình lục giác đều ban đầu (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid9-1767809168.png)