Cho tam giác\[ABC\] nhọn \(\left( {AB < AC} \right)\)nội tiếp đường tròn tâm \[O\]. Các đường cao \[BM\] và \[CN\]của tam giác\[ABC\] cắt nhau tại \[H\].
a) Chứng minh tứ giác \[BNMC\] nội tiếp và \[\widehat {ACB} = \widehat {AHM}\].
b) Tia \[AH\] cắt cạnh \[BC\] tại \[D\]. Trên tia \[DN\] lấy điểm \[E\] sao cho \[NE = ND\]. Gọi \[K\] là giao điểm của \[AD\] và \[NM\] và \[P\] là giao điểm của \[EK\] và \[AB\]. Chứng minh đường thẳng \[NM\] đi qua trung điểm của đoạn thẳng \[HP\].
Cho tam giác\[ABC\] nhọn \(\left( {AB < AC} \right)\)nội tiếp đường tròn tâm \[O\]. Các đường cao \[BM\] và \[CN\]của tam giác\[ABC\] cắt nhau tại \[H\].
a) Chứng minh tứ giác \[BNMC\] nội tiếp và \[\widehat {ACB} = \widehat {AHM}\].
b) Tia \[AH\] cắt cạnh \[BC\] tại \[D\]. Trên tia \[DN\] lấy điểm \[E\] sao cho \[NE = ND\]. Gọi \[K\] là giao điểm của \[AD\] và \[NM\] và \[P\] là giao điểm của \[EK\] và \[AB\]. Chứng minh đường thẳng \[NM\] đi qua trung điểm của đoạn thẳng \[HP\].
Quảng cáo
Trả lời:
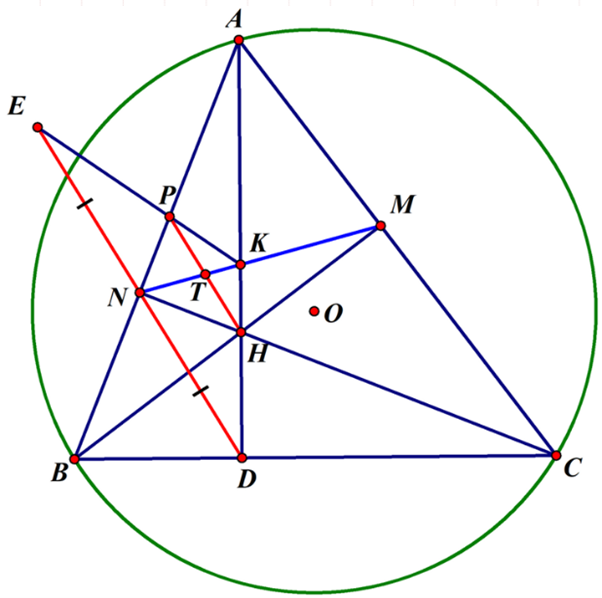
a) Ta có \(\widehat {BNC} = \widehat {BMC} = 90^\circ \) (gt).
Suy ra \(\Delta BNC\) và \(\Delta BMC\) nội tiếp đường tròn đường kính \[BC\].
Suy ra tứ giác \[BNMC\] nội tiếp đường tròn đường kính \[BC\].
Suy ra \(\widehat {ACB} = \widehat {ANM}\)(cùng bù với \[\widehat {BNM}\]) (1).
Chứng minh tương tự như trên ta có tứ giác \[BMHN\] nội tiếp đường tròn đường kính \[AH\],
suy ra \(\widehat {AHM} = \widehat {ANM}\)(hai góc nội tiếp cùng chắn ).
Từ (1) và (2) suy ra \[\widehat {ACB} = \widehat {AHM}\].
b) Ta có \[BM\] và \[CN\] là hai đường cao cắt nhau tại \[H\] của \[\Delta ABC\] nên \[H\] là trực tâm của \[\Delta ABC\]
Suy ra \[AH \bot BC\]tại \[D\].
Chứng minh tương tự như câu a) có tứ giác \[BNHD\] nội tiếp đường tròn đường kính \[BH\],
suy ra \(\widehat {HND} = \widehat {HBC}\)(hai góc nội tiếp cùng chắn ) (3).
Xét đường tròn đường kính \[BC\] có \(\widehat {HNK} = \widehat {HBC}\)(hai góc nội tiếp cùng chắn ) (4).
Từ (3) và (4) ta có \(\widehat {HND} = \widehat {HNK}\)
Suy ra \(\frac{{NK}}{{ND}} = \frac{{HK}}{{HD}}\)(Tính chất đường phân giác của tam giác) hay \(\frac{{NK}}{{NE}} = \frac{{HK}}{{HD}}\)(5)
Xét đường tròn đường kính \[BH\] có \(\widehat {BND} = \widehat {BHD}\)(hai góc nội tiếp cùng chắn ),
Mà \(\widehat {AHM} = \widehat {BHD} = \widehat {ANM}\), \(\widehat {BND} = \widehat {PNE}\)
Do đó \(\widehat {ANM} = \widehat {PNE}\),
Suy ra \(\frac{{NK}}{{NE}} = \frac{{PK}}{{PE}}\) (6).
Từ (5) và (6) suy ra \(\frac{{PK}}{{PE}} = \frac{{HK}}{{HD}}\), suy ra \[PH\parallel ED\](Định lý Ta-lét đảo).
Gọi \[T\] là giao của \[MN\]và \[PH\], ta có \(\frac{{TH}}{{ND}} = \frac{{KT}}{{KN}} = \frac{{TP}}{{NE}}\) (Hệ quả Định lý Ta-lét)
Lại có \[ND = NE\](gt) nên suy ra \[TH = TP\], suy ra \[T\] là trung điểm \[PH\]
Vậy đường thẳng \[NM\] đi qua trung điểm \[T\] của đoạn thẳng \[HP\].
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là B
Lời giải
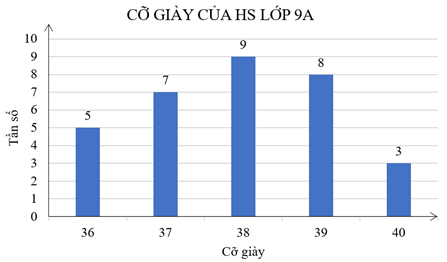
a) Ta bảng tần số của mẫu số liệu trên như sau:
|
Cỡ giày |
36 |
37 |
38 |
39 |
40 |
|
Tần số |
5 |
7 |
9 |
8 |
3 |
b) Ta có biểu đồ hình cột biểu diễn bảng tần số thu được ở câu a) như sau:
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(x < 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[{x^2} + 5x = 0\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.