Nghiệm của bất phương trình \[5 - 3x < - 1\] là

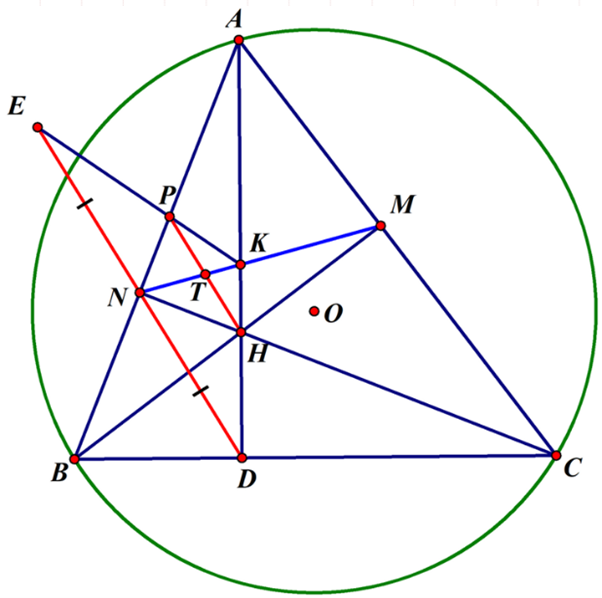
a) Ta có \(\widehat {BNC} = \widehat {BMC} = 90^\circ \) (gt).

Suy ra \(\Delta BNC\) và \(\Delta BMC\) nội tiếp đường tròn đường kính \[BC\].

Suy ra tứ giác \[BNMC\] nội tiếp đường tròn đường kính \[BC\].

Suy ra \(\widehat {ACB} = \widehat {ANM}\)(cùng bù với \[\widehat {BNM}\]) (1).

Chứng minh tương tự như trên ta có tứ giác \[BMHN\] nội tiếp đường tròn đường kính \[AH\],

suy ra \(\widehat {AHM} = \widehat {ANM}\)(hai góc nội tiếp cùng chắn ).

Từ (1) và (2) suy ra \[\widehat {ACB} = \widehat {AHM}\].

b) Ta có \[BM\] và \[CN\] là hai đường cao cắt nhau tại \[H\] của \[\Delta ABC\] nên \[H\] là trực tâm của \[\Delta ABC\]

Suy ra \[AH \bot BC\]tại \[D\].

Chứng minh tương tự như câu a) có tứ giác \[BNHD\] nội tiếp đường tròn đường kính \[BH\],

suy ra \(\widehat {HND} = \widehat {HBC}\)(hai góc nội tiếp cùng chắn ) (3).

Xét đường tròn đường kính \[BC\] có \(\widehat {HNK} = \widehat {HBC}\)(hai góc nội tiếp cùng chắn ) (4).

Từ (3) và (4) ta có \(\widehat {HND} = \widehat {HNK}\)

Suy ra \(\frac{{NK}}{{ND}} = \frac{{HK}}{{HD}}\)(Tính chất đường phân giác của tam giác) hay \(\frac{{NK}}{{NE}} = \frac{{HK}}{{HD}}\)(5)

Xét đường tròn đường kính \[BH\] có \(\widehat {BND} = \widehat {BHD}\)(hai góc nội tiếp cùng chắn ),

Mà \(\widehat {AHM} = \widehat {BHD} = \widehat {ANM}\), \(\widehat {BND} = \widehat {PNE}\)

Do đó \(\widehat {ANM} = \widehat {PNE}\),

Suy ra \(\frac{{NK}}{{NE}} = \frac{{PK}}{{PE}}\) (6).

Từ (5) và (6) suy ra \(\frac{{PK}}{{PE}} = \frac{{HK}}{{HD}}\), suy ra \[PH\parallel ED\](Định lý Ta-lét đảo).

Gọi \[T\] là giao của \[MN\]và \[PH\], ta có \(\frac{{TH}}{{ND}} = \frac{{KT}}{{KN}} = \frac{{TP}}{{NE}}\) (Hệ quả Định lý Ta-lét)

Lại có \[ND = NE\](gt) nên suy ra \[TH = TP\], suy ra \[T\] là trung điểm \[PH\]

Vậy đường thẳng \[NM\] đi qua trung điểm \[T\] của đoạn thẳng \[HP\].