Biết phương trình \({x^2} - 6x + 4 = 0\) có hai nghiệm \({x_1},\,\,{x_2}\). Không giải phương trình, tính giá trị của biểu thức \(T = {({x_1} + 2)^2} + {({x_2} + 2)^2}.\)

Với \[x \ge 0;x \ne 9\], ta có

\[A = \left( {\frac{{\sqrt x }}{{\sqrt x  + 3}} + \frac{3}{{\sqrt x  - 3}}} \right).\frac{{\sqrt x  + 3}}{{x + 9}}\]

\[ = \frac{{x + 9}}{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}.\frac{{\sqrt x  + 3}}{{x + 9}} = \frac{1}{{\sqrt x  - 3}}\]

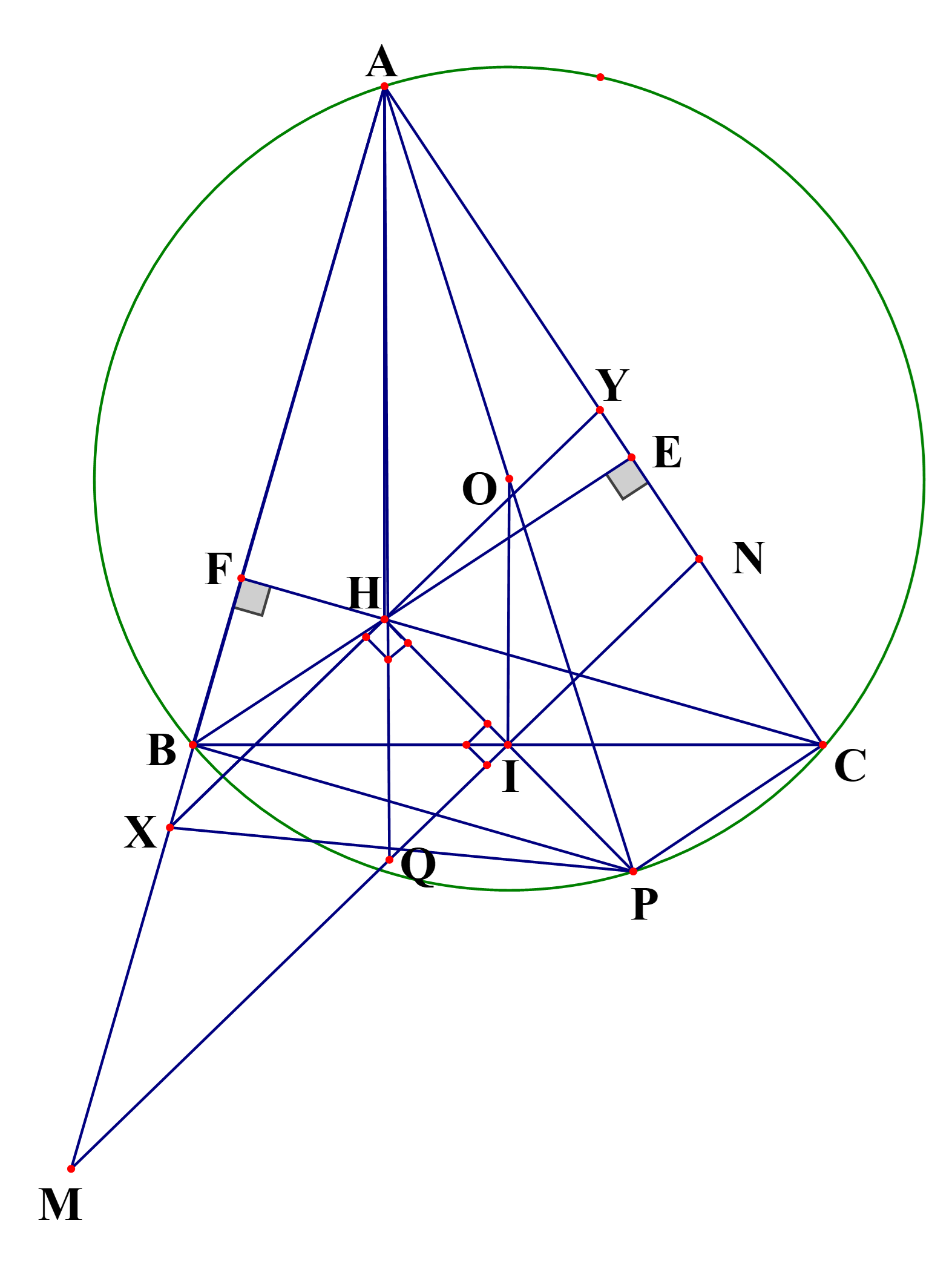
Suy ra 3 điểm \[B,E,C\] cùng nằm trên đường tròn đường kính BC (1).

Ta có: \[CF \bot AB\] nên \[\widehat {BFC} = 90^\circ .\]

Suy ra 3 điểm \[B,F,C\] cùng nằm trên đường tròn đường kính BC (2).

Từ (1) và (2) suy ra tứ giác \[BCEF\] nội tiếp.

b) Kẻ đường kính \[AP\] của đường tròn \[\left( O \right)\]. Khi đó \[PC \bot AC\] nên \[PC\]//\[BH\](cùng vuông góc với \[AC\]) và \[PB \bot AB\] nên \[PB\]//\[CH\](cùng vuông góc với \[AB\]). Do đó \[BHCP\] là hình bình hành.

Suy ra trung điểm \[I\]của \[BC\] cũng là trung điểm của \[PH\]. Vì vậy \[OI\] là đường trung bình của tam giác \[PAH\] nên \[OI = \frac{{AH}}{2}\] hay \[AH = 2OI\].

Kẻ đường thẳng qua \[H\], vuông góc với \[IH\]cắt các đường thẳng \[AB,AC\] lần lượt tại \[X,Y\].

Vì \[\widehat {PBX} = \widehat {PHX} = {90^o}\] nên các điểm \[P,B,X,H\] nằm trên đường tròn đường kính \[PX\], suy ra \[\widehat {PXH} = \widehat {PBH}\]. Tương tự \[\widehat {PCY} = \widehat {PHY} = {90^o}\] nên các điểm \[P,C,Y,H\] nằm trên đường tròn đường kính \[PY\], suy ra \[\widehat {PYH} = \widehat {PCH}\]

Mà \[BHCP\] là hình bình hành nên \[\widehat {PBH} = \widehat {PCH}\], suy ra \[\widehat {PXH} = \widehat {PYH}\] hay tam giác \[PXY\] cân tại \[P\], đường cao \[PH\] nên \[H\] là trung điểm của \[XY\].

Vì \[XY\]//\[MN\] nên ta có \[\frac{{XH}}{{MQ}} = \frac{{AH}}{{AQ}} = \frac{{HY}}{{QN}}\]. Suy ra \[MQ = QN\] hay \[Q\] là trung điểm của \[MN\]