Cho hai biểu thức \(A = \frac{{2\sqrt x - 3}}{{\sqrt x - 1}}\) và \(B = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{5}{{\sqrt x + 1}} - \frac{{8\sqrt x - 6}}{{x - 1}}\) với \(x \ge 0,x \ne 1\)
1) Tính giá trị biểu thức \(A\) khi \(x = 9\)
2) Rút gọn biểu thức \(B\)
3) Tìm giá trị của \(x\) để \(P = A.B\) đạt giá trị nguyên lớn nhất
Cho hai biểu thức \(A = \frac{{2\sqrt x - 3}}{{\sqrt x - 1}}\) và \(B = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{5}{{\sqrt x + 1}} - \frac{{8\sqrt x - 6}}{{x - 1}}\) với \(x \ge 0,x \ne 1\)
1) Tính giá trị biểu thức \(A\) khi \(x = 9\)
2) Rút gọn biểu thức \(B\)
3) Tìm giá trị của \(x\) để \(P = A.B\) đạt giá trị nguyên lớn nhất
Quảng cáo
Trả lời:
1) Khi \(x = 9\left( {tm} \right)\) giá trị biểu thức \(A\) là :
\(A = \frac{{2.\sqrt 9 - 3}}{{\sqrt 9 - 1}}\)\( = \frac{{6 - 3}}{{3 - 1}}\)\( = \frac{3}{2}\)
Vậy \(A = \frac{3}{2}\)khi \(x = 9\)
2) \(B = \frac{{\sqrt x }}{{\sqrt x - 1}} + \frac{5}{{\sqrt x + 1}} - \frac{{8\sqrt x - 6}}{{x - 1}}\)\( = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{{5\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}} - \frac{{8\sqrt x - 6}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\)
\( = \frac{{x + \sqrt x + 5\sqrt x - 5 - 8\sqrt x + 6}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\)\( = \frac{{x - 2\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\)\( = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\)\[ = \frac{{\sqrt x - 1}}{{\sqrt x + 1}}\]
3) \(P = A.B\)\( = \frac{{2\sqrt x - 3}}{{\sqrt x - 1}}.\frac{{\sqrt x - 1}}{{\sqrt x + 1}}\)\( = \frac{{2\sqrt x - 3}}{{\sqrt x + 1}}\)\( = \frac{{2\left( {\sqrt x + 1} \right) - 5}}{{\sqrt x + 1}}\)\( = 2 - \frac{5}{{\sqrt x + 1}}\)
+) Với \(x \ge 0\) ta có \(\sqrt x + 1 > 0\)\( \Rightarrow \frac{{ - 5}}{{\sqrt x + 1}} < 0\)\( \Rightarrow 2 - \frac{5}{{\sqrt x + 1}} < 2\)\( \Rightarrow P < 2\) (1)
+) Với \(x \ge 0\) ta có \(\sqrt x + 1 \ge 1\)\( \Rightarrow \frac{{ - 5}}{{\sqrt x + 1}} \ge - 5\)\( \Rightarrow 2 - \frac{5}{{\sqrt x + 1}} \ge - 3\)\( \Rightarrow P \ge - 3\) (2)
Từ (1) và (2) ta có \( \Rightarrow - 3 \le P < 2\), mà \(P \in \mathbb{Z}\), \(P\,m{\rm{ax}}\) nên \(P\, = 1\)
\(2 - \frac{5}{{\sqrt x + 1}} = 1\)\( \Rightarrow \frac{5}{{\sqrt x + 1}} = 1\)\( \Rightarrow \sqrt x + 1 = 5\)\( \Rightarrow x = 16\left( {tm} \right)\)
Vậy \(x = 16\)là giá trị cần tìm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
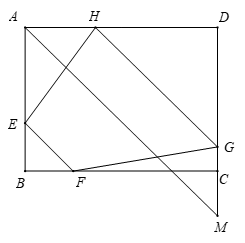
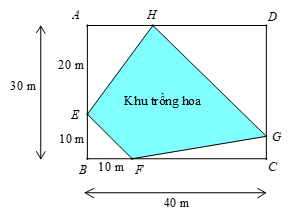
Gọi độ dài \(AH = x\,\left( {\rm{m}} \right)\) với \(0 < x < 40\). Khi đó \(HD = 40 - x\,\left( {\rm{m}} \right)\)
Qua \(A\) kẻ đường thẳng song song với \(EF\) cắt \(DC\) tại \(M\)
Khi đó \(\widehat {DHG} = \widehat {DAM} = \widehat {BEF} = 45^\circ \)
Do đó tam giác \(DHG\) vuông cân tại \(D\)
Suy ra \(DH = DG = 40 - x\,\left( {\rm{m}} \right)\)
Như vậy \(GC = DC - DG = 30 - \left( {40 - x} \right) = x - 10\,\left( {\rm{m}} \right)\)
Ta có: \({S_{AHE}} = \frac{1}{2}\, \cdot AH\, \cdot \,AE = \frac{1}{2}\, \cdot \,x \cdot 20 = 10x\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
\({S_{DHG}} = \frac{1}{2}\, \cdot DH\, \cdot DG = \frac{1}{2}\, \cdot \,{\left( {40 - x} \right)^2}\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
\({S_{FCG}} = \frac{1}{2}\, \cdot CG\, \cdot \,CF = \frac{1}{2}\, \cdot \,\left( {x - 10} \right)\, \cdot \,\left( {40 - 10} \right) = 15\left( {x - 10} \right)\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
\({S_{EFGH}} = {S_{ABCD}} - \left( {{S_{EBF}} + {S_{AEH}} + {S_{HDG}} + {S_{FGC}}} \right)\)
Đặt \(P = {S_{AEH}} + {S_{HDG}} + {S_{FGC}}\)
Ta cần tìm giá trị nhỏ nhất của \(P = 10x + \frac{{{{\left( {40 - x} \right)}^2}}}{2} + 15\left( {x - 10} \right)\)
\(P = 10x + \frac{{{x^2} - 80x + 1600}}{2} + 15x - 150\)
\(P = \frac{{{x^2}}}{2} - 15x + 650\)
\(2P = {x^2} - 30x + 1300\)
\[2P = {\left( {x - 15} \right)^2} + 1075 \ge 1075\]
Do đó \(P \ge 537,5\)
Dấu xảy ra khi \(x = 15\) (thỏa mãn điều kiện)
Vậy diện tích lớn nhất của mảnh đất trồng hoa là \(30\,.\,40 - \frac{1}{2}\, \cdot \,{10^2} - 537,5 = 612,5\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Lời giải
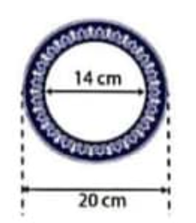
1) Bán kính lớn của viên trắng men xanh của đĩa sứ là \(20:2 = 10\) cm
Bán kính nhỏ của viên trắng men xanh của đĩa sứ là \(14:2 = 7\) cm
Diện tích phần viên trắng men xanh của đĩa sứ là
\(\pi ({R^2} - {r^2}) = \pi ({10^2} - {7^2}) \approx 160(c{m^2})\)
Vậy diện tích phần viên trắng men xanh của đĩa sứ khoảng \(160c{m^2}\)
2)
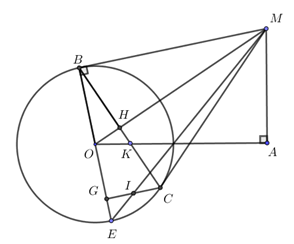
a) \(M,A,B,O\) cùng thuộc 1 đường tròn
\( \Rightarrow \Delta MAO\) vuông tại \(A\) \( \Rightarrow M,A,O\) thuộc đường tròn đường kính \(OM\) \((1)\)
\( \Rightarrow \Delta MBO\) vuông tại \(B\) \( \Rightarrow M,B,O\) thuộc đường tròn đường kính \(OM\) \((2)\)
Từ \((1),(2)\) \( \Rightarrow MABO\) cùng thuộc đường tròn đường kính \(OM\)
b) Xét \(\Delta MBO\) và \(\Delta MCO\) có:
\(MB = MC\) (\(M\) thuộc trung trực của \(BC\))
\(OB = OC( = R)\)
\( \Rightarrow \Delta MBO = \Delta MCO(c.c.c)\)
\( \Rightarrow MCO = MBO = 90^\circ \)
\( \Rightarrow MC \bot OC\) tại \(C \in (O)\)
\( \Rightarrow MC\) là tiếp tuyến của \((O)\)
• \((g.g)\) \( \Rightarrow \frac{{OK}}{{OM}} = \frac{{OH}}{{OA}}\) \( \Rightarrow OK \cdot OA = OH \cdot OM\)
• \((g.g)\) \( \Rightarrow \frac{{OH}}{{OB}} = \frac{{OB}}{{OM}}\) \( \Rightarrow OH \cdot OM = O{B^2} = {R^2}\)
\( \Rightarrow OK \cdot OA = OH \cdot OM = {R^2}\)
c) Vì \(GI\,{\rm{//}}\,BM\) \( \Rightarrow \frac{{BM}}{{GI}} = \frac{{BE}}{{GE}} \Rightarrow \frac{{BM}}{{2GI}} = \frac{{2BO}}{{2GE}} \Rightarrow \frac{{BM}}{{2GI}} = \frac{{BO}}{{GE}}(3)\)
(gg) \( \Rightarrow \frac{{BO}}{{GE}} = \frac{{BM}}{{GC}}\) (4)
Từ (3)(4) \( \Rightarrow \frac{{BM}}{{2GI}} = \frac{{BM}}{{GC}}\)\( \Rightarrow GC = 2GI\)\( \Rightarrow I\) là trung điểm của \(GC\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.